Scorte di sicurezza

Le scorte di sicurezza sono un metodo di ottimizzazione delle scorte che indica quanto inventario deve essere mantenuto oltre la domanda prevista al fine di raggiungere un determinato obiettivo di livello di servizio. Lo stock extra funge da buffer “di sicurezza” - da qui il nome - per proteggere l’azienda dalle future fluttuazioni previste. La formula delle scorte di sicurezza dipende sia dalla domanda futura prevista che dal tempo di consegna futuro previsto. L’incertezza viene considerata distribuita normalmente per entrambi i fattori. La formula delle scorte di sicurezza è ubiquitaria nella maggior parte dei sistemi di gestione delle scorte, compresi i più noti ERP e MRP.

Aggiornamento luglio 2020: L’approccio dettagliato di seguito è la “teoria” della supply chain, purtroppo, si rivela anche estremamente disfunzionale. In particolare, né la domanda futura né il tempo di consegna futuro sono distribuiti normalmente (cioè non sono gaussiani). Inoltre, l’intera prospettiva perde completamente il punto che tutti gli SKU che possono essere ordinati o prodotti dall’azienda competono per le stesse risorse. Sconsigliamo vivamente di utilizzare qualsiasi modello di scorte di sicurezza per quanto riguarda le vere supply chain.

Pubblico di destinazione: Questo documento è principalmente destinato a professionisti della supply chain nel settore del commercio al dettaglio o della produzione. Tuttavia, questo documento è anche utile per gli editori di software di contabilità / ERP / eCommerce che desiderano estendere le loro applicazioni con funzionalità di gestione delle scorte.

Abbiamo cercato di mantenere il requisito matematico il più basso possibile, tuttavia non possiamo evitare del tutto tutte le formule poiché lo scopo preciso di questo documento è essere una guida pratica che spiega come calcolare le scorte di sicurezza.

Download: calcola-scorte-di-sicurezza.xls (Foglio di calcolo Microsoft Excel)

Introduzione

La gestione delle scorte è un trade-off finanziario tra i costi delle scorte e i costi di stock-out. Più scorte ci sono, più capitale circolante è necessario e maggiore è la svalutazione delle scorte. D’altra parte, se non si dispone di abbastanza scorte, si verificano stock-out delle scorte, mancando potenziali vendite, possibilità di interrompere l’intero processo produttivo.

Le scorte di magazzino dipendono essenzialmente da due fattori

• domanda nel lead time: la quantità di articoli che verranno consumati o acquistati.
• tempo di consegna: il ritardo tra la decisione di riordinare e la disponibilità rinnovata.

Tuttavia, questi due fattori sono soggetti a incertezze

• variazioni della domanda: i comportamenti dei clienti possono evolvere in modi piuttosto imprevedibili.
• variazioni del tempo di consegna: i fornitori o i trasportatori possono trovarsi di fronte a difficoltà impreviste.

Decidere il livello delle scorte di sicurezza è implicitamente equivalente a fare un trade-off tra questi costi considerando le incertezze.

L’equilibrio tra i costi delle scorte e i costi degli stock-out dipende molto dall’attività aziendale. Pertanto, anziché considerare direttamente questi costi, introdurremo ora la classica nozione di livello di servizio.

Il livello di servizio esprime la probabilità che un certo livello di scorte di sicurezza non porti a stock-out. Naturalmente, quando le scorte di sicurezza aumentano, aumenta anche il livello di servizio. Quando le scorte di sicurezza diventano molto grandi, il livello di servizio tende al 100% (cioè probabilità zero di incontrare stock-out).

Scegliere il livello di servizio, cioè la probabilità accettabile di stock-out, esula dallo scopo di questa guida, ma abbiamo una guida separata su come calcolare i livelli di servizio ottimali.

Modello di riapprovvigionamento delle scorte

Il punto di riordino è la quantità di scorte che dovrebbe innescare un ordine. Se non ci fosse incertezza (cioè se la domanda futura fosse perfettamente nota e l’approvvigionamento fosse perfettamente affidabile), il punto di riordino sarebbe semplicemente uguale alla domanda prevista totale durante il tempo di consegna, chiamata anche domanda durante il tempo di consegna.

In pratica, a causa delle incertezze, abbiamo

punto di riordino = domanda durante il tempo di consegna + scorte di sicurezza

Se assumiamo che le previsioni non siano sbilanciate (statisticamente parlando), avere scorte di sicurezza pari a zero porterebbe a un livello di servizio del 50%. Infatti, previsioni non sbilanciate significano che c’è la stessa probabilità che la domanda futura sia maggiore o minore della domanda durante il tempo di consegna (ricordiamo che la domanda durante il tempo di consegna è solo un valore previsto).

Attenzione: le previsioni possono essere non sbilanciate senza essere esatte. Il bias indica un errore sistematico del modello di previsione (ad esempio, sovrastimare sempre la domanda del 20%).

Distribuzione normale dell’errore

A questo punto, abbiamo bisogno di un modo per rappresentare l’incertezza nella domanda durante il tempo di consegna. In seguito, supporremo che l’errore sia distribuito normalmente, guarda l’immagine qui sotto.

Note statistiche: questa assunzione di distribuzione normale non è del tutto arbitraria. In determinate situazioni, gli stimatori statistici convergono a una distribuzione normale come indicato dal teorema del limite centrale. Ma queste considerazioni esulano dallo scopo di questa guida.

Una distribuzione normale è definita solo da due parametri: la sua media e la sua varianza. Poiché assumiamo che le previsioni siano non sbilanciate, assumiamo che la media della distribuzione dell’errore sia zero, il che non significa che stiamo assumendo un errore pari a zero.

Determinare la varianza dell’errore di previsione è un compito più delicato. Lokad, come la maggior parte degli strumenti di previsione, fornisce stime MAPE (Mean Absolute Percentage Error) associate alle sue previsioni. Per completezza, spiegheremo come euristiche semplici possono essere utilizzate per superare questo problema.

In particolare, la varianza all’interno dei dati storici può essere utilizzata come buona euristica per stimare la varianza dell’errore di previsione. David Piasecki suggerisce anche di utilizzare la domanda prevista invece della domanda media nell’espressione della varianza, cioè

dove $$E$$ è l’operatore media, $$y_t$$ è la domanda storica per il periodo $$t$$ (tipicamente la quantità di vendite) e $$y’$$ la domanda prevista.

L’idea chiave dietro questa assunzione è che l’errore di previsione è molto spesso correlato alla quantità di variazione prevista: maggiore sono le variazioni imminenti, maggiore è l’errore nelle previsioni.

In realtà, il calcolo di questa varianza dell’errore comporta alcune sottigliezze che saranno trattate in maggior dettaglio di seguito.

Espressione del stock di sicurezza

A questo punto, abbiamo determinato sia la media che la varianza, quindi la distribuzione dell’errore è nota. Dobbiamo ora calcolare il livello di errore accettabile all’interno di questa distribuzione. Qui sopra, abbiamo introdotto la nozione di livello di servizio (una percentuale) per farlo.

Note: Stiamo assumendo un tempo di approvvigionamento statico. Tuttavia, un approccio molto simile può essere utilizzato per un tempo di approvvigionamento variabile. Vedi

• Comprensione dei tempi di approvvigionamento variabili
• Modellazione dei tempi di approvvigionamento variabili

Per convertire il livello di servizio in un livello di errore, chiamato anche fattore di servizio, dobbiamo utilizzare la distribuzione normale cumulativa inversa (a volte chiamata anche distribuzione normale inversa) (vedi NORMSINV per la corrispondente funzione Excel). Anche se potrebbe sembrare complicato, non lo è, suggeriamo di dare un’occhiata all’applet sulla distribuzione normale per avere una visione più visuale. Come puoi vedere, la funzione cumulativa trasforma la percentuale in un’area sotto la curva, la soglia sull’asse X corrisponde al valore del fattore di servizio.

In modo intuitivo, calcoliamo

stock di sicurezza = deviazione standard dell'errore * fattore di servizio

Più formalmente, sia $$S$$ il stock di sicurezza, abbiamo

dove $$\sigma$$ è la deviazione standard (cioè la radice quadrata di $$\sigma^2$$ la varianza definita qui sopra), $$cdf$$ la distribuzione normale cumulativa normalizzata (media zero e varianza pari a uno) e $$P$$ il livello di servizio.

Ricordando che

punto di riordino = domanda durante il tempo di approvvigionamento + stock di sicurezza

Sia $$R$$ il punto di riordino, abbiamo

Abbinamento tra tempo di approvvigionamento e periodo di previsione

Finora, abbiamo semplicemente supposto che per un determinato tempo di approvvigionamento, fossimo in grado di produrre direttamente la corrispondente previsione della domanda futura. Nella pratica, non funziona esattamente così. L’analisi dei dati storici di solito inizia aggregando i dati in periodi di tempo (tipicamente settimane o mesi).

Tuttavia, il periodo scelto potrebbe non corrispondere esattamente al tempo di approvvigionamento; quindi, sono necessari ulteriori calcoli per esprimere la domanda durante il tempo di approvvigionamento e la sua varianza associata (considerando che stiamo ancora assumendo una distribuzione normale per l’errore di previsione, come dettagliato nella sezione precedente).

In modo intuitivo, la domanda durante il tempo di approvvigionamento può essere calcolata come la somma dei valori previsti per i periodi futuri che si sovrappongono al segmento di tempo di approvvigionamento. Bisogna fare attenzione ad aggiustare correttamente l’ultimo periodo previsto.

Formalmente, sia $$T$$ il periodo e $$L$$ il tempo di approvvigionamento. Scriviamo

dove $$k$$ è un numero intero e $$0 ≤ α < 1$$. Sia $$D$$ la domanda durante il tempo di approvvigionamento. Allora, abbiamo l’espressione finale per la domanda durante il tempo di approvvigionamento

dove $$y’_n$$ è la domanda prevista per l’$$n^{esimo}$$ periodo futuro.

Considerando le stesse ipotesi sulla distribuzione normale, possiamo calcolare la varianza dell’errore di previsione come

dove $$y’$$ è la previsione media per periodo

Tuttavia, $$\sigma^2$$ viene calcolato qui come una varianza per periodo mentre avremmo bisogno di una varianza che corrisponda al tempo di approvvigionamento. Sia $$\sigma_{L}^2$$ la varianza per tempo di approvvigionamento aggiustata, abbiamo

Infine, possiamo riepilogare il punto di riordino come

Utilizzare Excel per calcolare il punto di riordino

In questa sezione viene spiegato come calcolare il punto di riordino con Microsoft Excel. Suggeriamo di dare un’occhiata al foglio di calcolo Excel di esempio fornito.

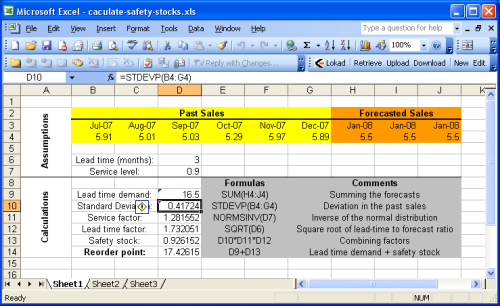
Il foglio di calcolo di esempio è essenzialmente diviso in due sezioni: le ipotesi in alto e i calcoli in basso. Le previsioni sono considerate parte delle ipotesi perché la previsione delle vendite (o della domanda) esula dallo scopo di questa guida. Puoi fare riferimento al nostro tutorial per la previsione delle vendite con Microsoft Excel per ulteriori dettagli.

La maggior parte delle formule introdotte nella sezione precedente sono operazioni molto semplici (addizioni, moltiplicazioni) che sono molto facili da eseguire con Microsoft Excel. Tuttavia, due funzioni sono degne di nota

• NORMSINV (Microsoft KB): stima la distribuzione normale cumulativa, indicata come cdf qui sopra.
• STDEV (Microsoft KB): stima la deviazione standard, indicata come $$σ$$ qui sopra. Ricordiamo che la deviazione standard $$σ$$ è la radice quadrata della varianza $${σ^2}$$.

Per semplicità, il primo foglio di calcolo non implementa l’euristica $${σ^2 = E[ (y_t - y’)^2 ]}$$ nel calcolo del fattore di servizio. Questo approccio è implementato in Sheet2 (secondo foglio di calcolo del documento Excel). Poiché abbiamo ipotizzato previsioni stazionarie nell’esempio, il punto di riordino rimane identico con o senza questa euristica.

Risorse

Inventory Management and Production Planning and Scheduling, Edward A. Silver, David F. Pyke, Rein Peterson, Wiley; 3a edizione, 1998