Réapprovisionnement priorisé des stocks dans Excel avec des prévisions probabilistes

Par Alexey Tikhonov, Fabian Hoehner et Conor Doherty, janvier 2023

L’incertitude est un aspect inévitable de la prévision. Pourtant, au XXe siècle, la prévision statistique est apparue avec l’espoir que, grâce à des modèles mathématiques adéquats, l’incertitude pourrait être éliminée. En conséquence, les premières théories de la chaîne d’approvisionnement ont minimisé ou rejeté l’incertitude, car on s’attendait à ce que de nouvelles techniques de prévision meilleures éliminent cette incertitude ou, à défaut, la rendent insignifiante. Bien que bien intentionnées, ces approches étaient défectueuses car l’incertitude, après un siècle de modélisation statistique, reste résolument inéliminable. En 2012, Lokad a pionnier une perspective de chaîne d’approvisionnement alternative, qui embrasse et quantifie l’incertitude. Cette approche utilise des prévisions probabilistes au lieu des prévisions classiques de séries chronologiques. Dans ce guide, et la feuille de calcul Microsoft Excel qui l’accompagne, nous appliquons des prévisions probabilistes au problème de réapprovisionnement des stocks. Cette approche aboutit à une politique de réapprovisionnement des stocks priorisée, ici démontrée à travers Excel. Notre intention est double : premièrement, populariser cette approche auprès d’un public qui pourrait ne pas être à l’aise avec des outils logiciels plus avancés ; et deuxièmement, démontrer que l’acceptation de l’incertitude nécessite plus une certaine mentalité qu’un outil sophistiqué.

Télécharger : probabilistic-inventory-replenishment.xlsx

1. Le problème de réapprovisionnement des stocks

Le problème de réapprovisionnement des stocks consiste à identifier la meilleure liste d’achats - celle qui tient compte des contraintes financières et des objectifs principaux de l’entreprise. La méthode pour produire une telle liste devrait fonctionner également bien indépendamment des contraintes budgétaires, étant donné que la méthode vise à maximiser le retour sur investissement pour chaque dollar dépensé. Le problème est que tous les SKUs sont en concurrence pour les mêmes dollars, donc le retour financier de la mise en stock de chaque unité d’un SKU donné doit être quantifié et classé dans le contexte de toutes les unités supplémentaires de chaque SKU.

1.1 La solution de réapprovisionnement priorisé des stocks

Le processus de classement des stocks, tel que décrit ci-dessus, nécessite une perspective microscopique. Afin de comparer le retour de l’ajout de chaque unité d’un SKU donné à une liste d’achats, plusieurs facteurs doivent être pris en compte. Notamment, la probabilité de vente fournie par une prévision de la demande probabiliste et les moteurs économiques - tels que la marge brute et le prix d’achat. Chaque quantité considérée doit à son tour être équilibrée par rapport aux contraintes internes et externes (telles que la capacité limitée de l’entrepôt, les multiplicateurs de lots et les MOQs/MOVs, etc.). Les cas particuliers, tels que lorsque deux (ou plus) unités ont une rentabilité attendue égale, doivent être pris en compte dans une politique de réapprovisionnement des stocks grâce à l’évaluation de l’importance relative de chaque produit. Les SKUs ne doivent pas être considérés de manière isolée, mais plutôt en paniers. Certains SKUs, malgré des marges bénéficiaires plus faibles pris individuellement (comme le lait), sont plus importants car ils permettent des ventes de produits à marge élevée. Ainsi, la récompense financière pour maintenir les niveaux de service d’un produit à marge inférieure - celui qui facilite d’autres ventes - représente un autre moteur (“couverture de rupture de stock”)¹. Une approche de réapprovisionnement priorisé des stocks (PIR), utilisant une prévision probabiliste comme entrée, prend en compte tous les facteurs décrits ci-dessus.

En résumé, la solution PIR peut être résumée en trois étapes :

1. Établir une prévision de la demande probabiliste.

2. Énumérer toutes les quantités d’achat réalisables.

3. Classer toutes les quantités d’achat réalisables en fonction des moteurs économiques.

1.2 Réapprovisionnement priorisé des stocks dans Excel

En utilisant des données financières pour un magasin fictif, y compris les moteurs économiques énumérés dans la section précédente, cette feuille de calcul Excel modélise la politique de réapprovisionnement des stocks pour trois SKUs (stylos, claviers et bibliothèques)². Les conséquences financières de chaque unité supplémentaire de SKU (si commandée), et la probabilité de la vendre, sont illustrées dans la feuille Graphiques (voir Figure 1). Les diagrammes et graphiques se mettront à jour en fonction des entrées et des hypothèses du modèle (par exemple, niveaux de stock initiaux, prix d’achat et de vente, etc.) dans la feuille Tour de contrôle (Figure 2). Une liste détaillée des options de décision réalisables est générée dans la feuille Décisions d’achat microscopiques (Figure 3) en fonction des principales entrées. Ces entrées sont les prévisions de demande probabilistes de la feuille Générateurs de distribution (Figure 4) et les entrées de la feuille Tour de contrôle. Enfin, un tableau de décisions de réapprovisionnement des stocks priorisées est compilé et classé en termes de retour sur investissement attendu (voir la feuille Décisions d’achat classées dans la Figure 5).

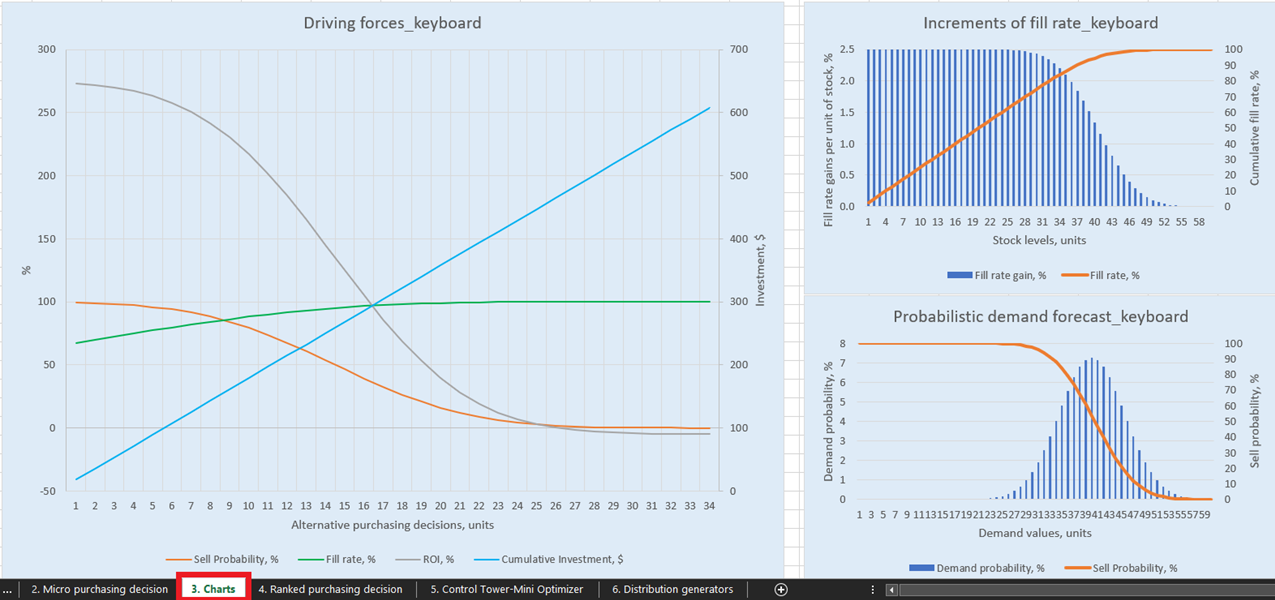
Figure 1. Vue du clavier des forces motrices dans Charts, emplacement surligné en rouge.

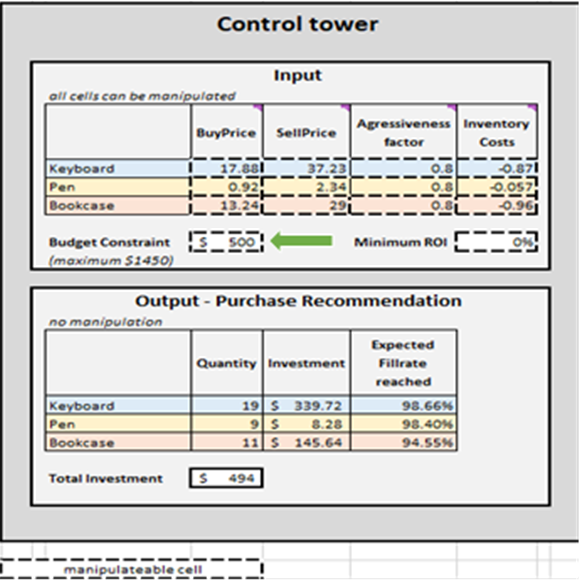
Figure 2. Vue de la "Tour de contrôle" située dans Tour de contrôle - Mini Optimizer (feuille 5). On peut modifier la "Contrainte budgétaire" à n'importe quelle valeur entre 0 $ et 1450 $ (voir flèche verte).

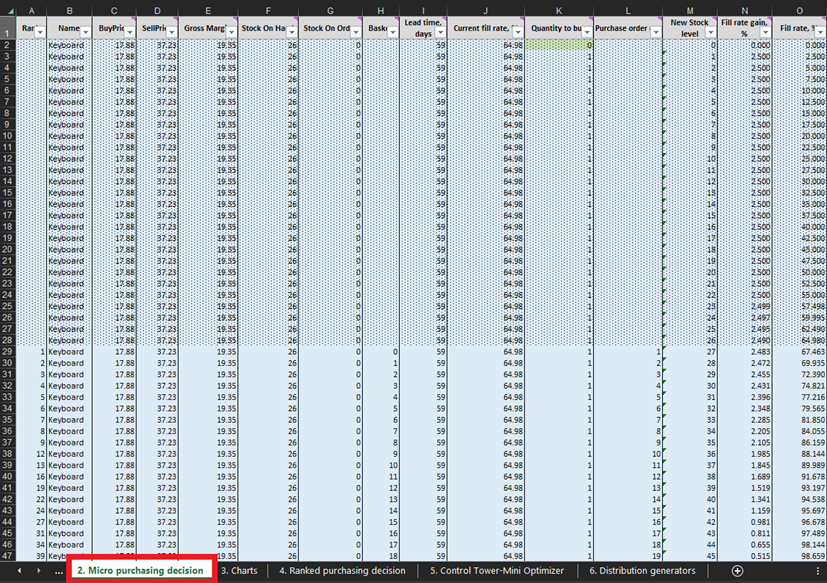
where-to-locate-micro-purchasing-decision-within-excel

Figure 3. Où localiser les décisions d'achat micro dans Excel, surligné en rouge. Les lignes couvertes par le formatage conditionnel en pointillés sont des données passées (jusqu'à la ligne 28 incluse dans l'image ci-dessus). Ces informations représentent les décisions d'achat précédentes. Nous nous intéressons uniquement à tout ce qui se trouve en dessous de ce formatage conditionnel. Le même formatage en pointillés s'applique aux données du stylo et de la bibliothèque.

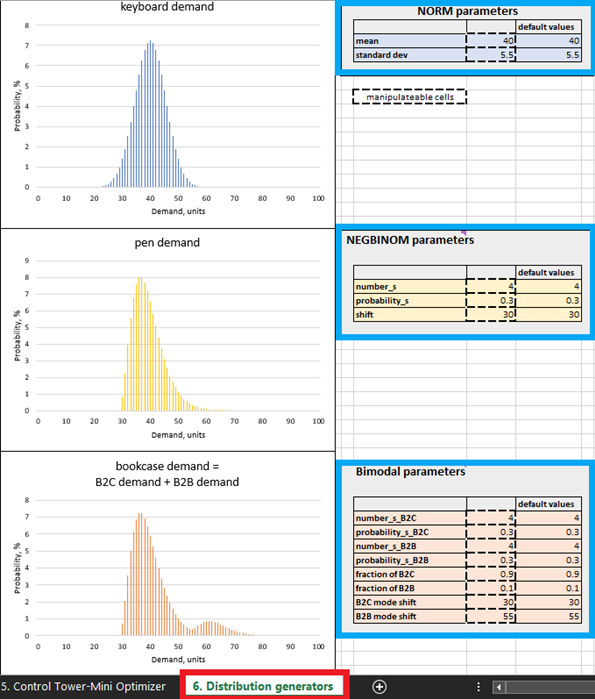
Figure 4. Où localiser les générateurs de distribution dans Excel, surligné en rouge. Les panneaux de contrôle des produits sont surlignés en bleu. Les cellules avec des contours en pointillés peuvent être manipulées.

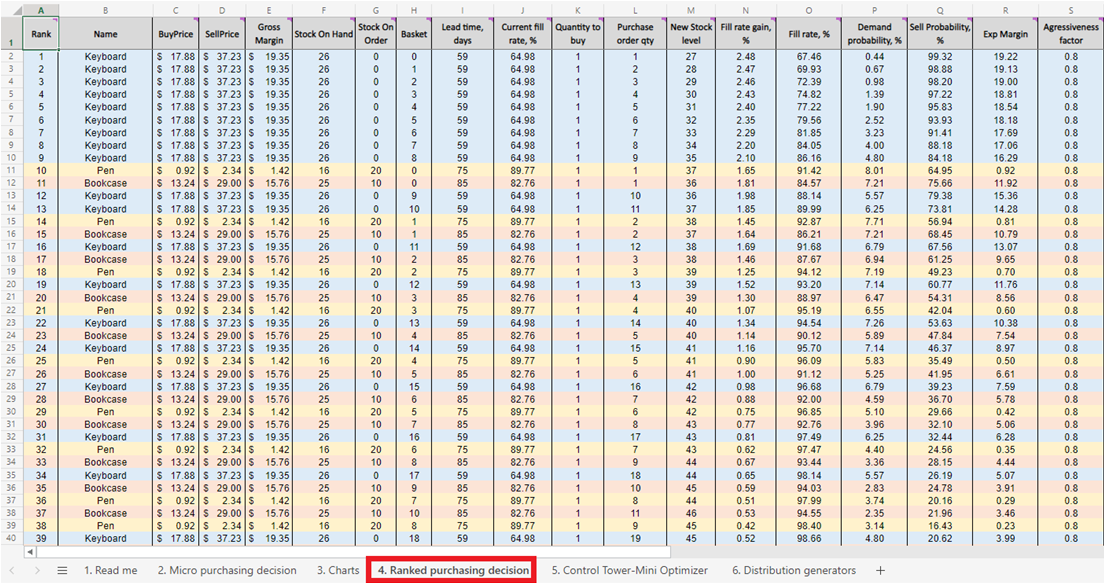
Figure 5. Une liste de réapprovisionnement des stocks priorisée des décisions d'achat micro, située dans la feuille 4.

2. Prévision de la demande probabiliste

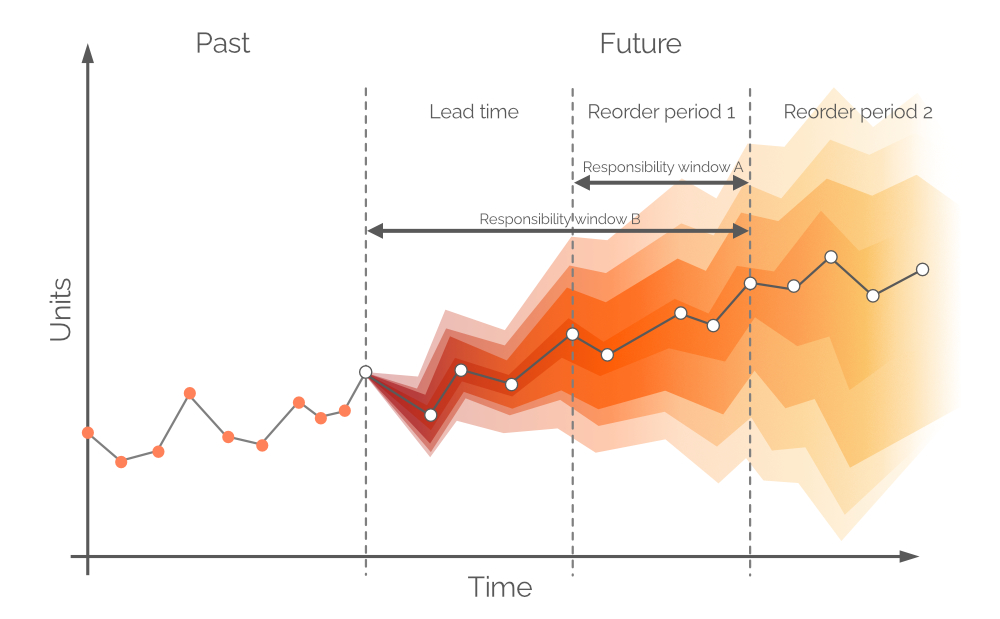
Dans ce contexte, une prévision probabiliste est un ensemble de toutes les valeurs de demande future probables et de leurs probabilités respectives. Elle intègre l’incertitude inhérente à la demande future et peut être établie sur n’importe quelle période de temps. Comme une prévision traditionnelle des séries temporelles, il existe une seule valeur de demande la plus probable identifiée (les points blancs dans la Figure 6) et une ligne de tendance (la ligne grise reliant les points blancs). Cependant, une prévision probabiliste intègre l’incertitude grâce à l’ajout de toutes les valeurs de demande possibles (bien qu’elles ne soient pas également probables). Cette approche est visible dans la Figure 6, où différents intervalles de confiance représentent des valeurs de demande avec différentes probabilités.

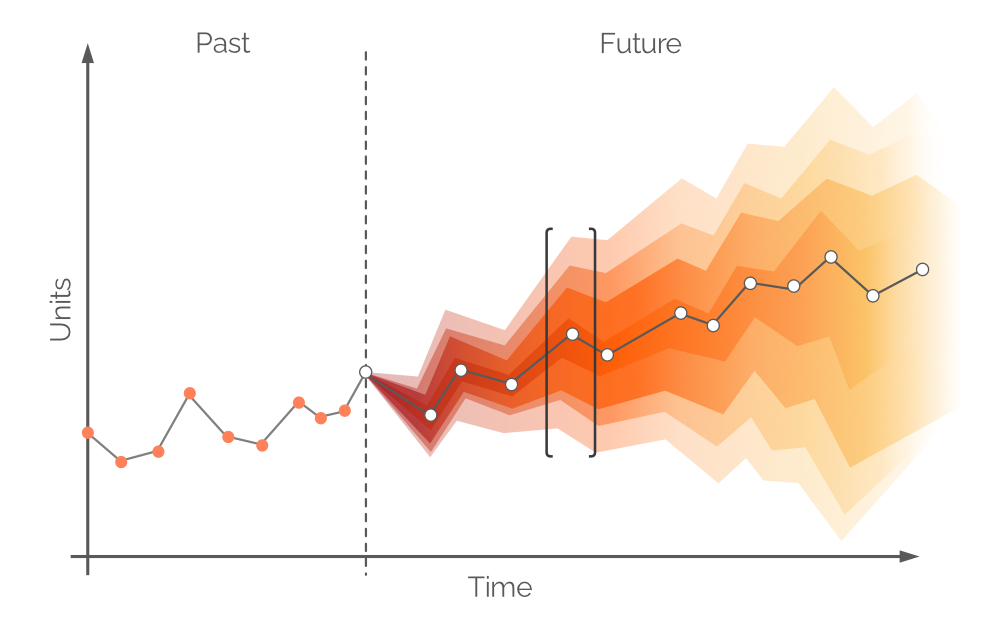
Figure 6. Une prévision probabiliste (demande sur l'axe des y ; temps sur l'axe des x). La ligne verticale grise en pointillés indique le moment présent ("maintenant"). Le temps est mesuré en jours, mais cela pourrait être n'importe quel intervalle souhaité. La zone entre les crochets noirs sera discutée ultérieurement.

Les points blancs dans la Figure 6 représentent les valeurs de demande les plus probables à des intervalles futurs fixes. Il y a une bande de couleur correspondant à une gamme de valeurs de demande futures alternatives - une distribution de probabilité en couleur. Cette couleur s’estompe le long de l’axe vertical plus on s’éloigne du point blanc, ce qui représente une plus grande incertitude et une probabilité plus faible. Dans l’ensemble, les bandes de couleur s’estompent à mesure que le temps avance (le long de l’axe horizontal), car l’incertitude s’intensifie avec le temps qui passe. Cependant, quel que soit l’incertitude, il y a toujours au moins une valeur qui est la plus probable, et cela est représenté en permanence par les points blancs. Un exemple de distribution de probabilité pour un point temporel est illustré dans la Figure 7.

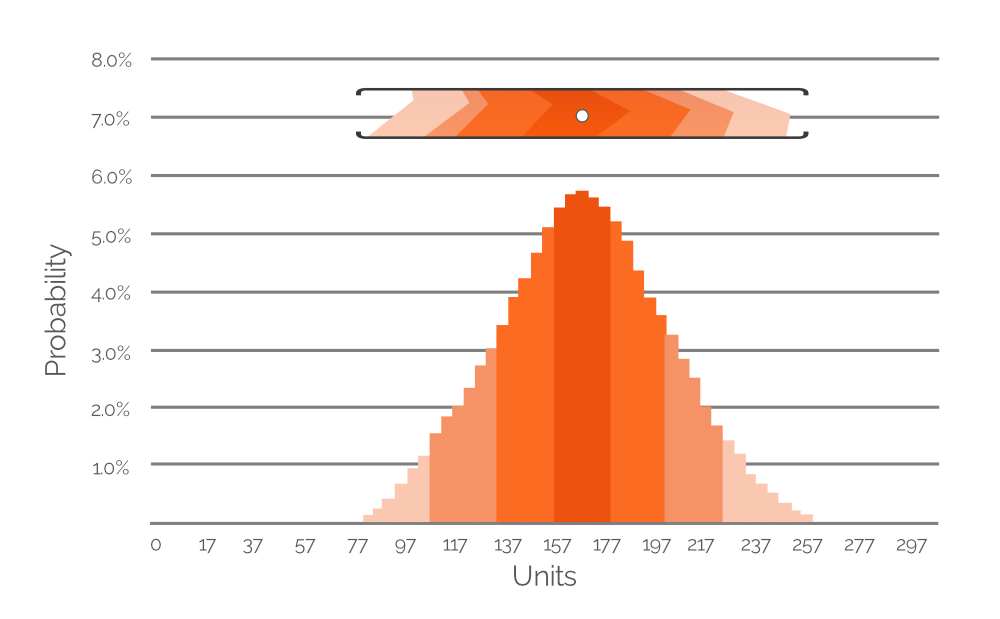
Figure 7. Un histogramme représentant la probabilité de plusieurs valeurs de demande possibles (par intervalles de 20 unités). L'axe des y représente la valeur de probabilité ; l'axe des x représente la demande en unités. L'histogramme est une représentation de la plage de valeurs surlignée dans la Figure 6 (incluse ici à titre de référence).

La Figure 7 exprime les données surlignées de la Figure 6 sous la forme d’un histogramme de probabilité, avec des valeurs numériques explicites indiquant la probabilité de différentes valeurs de demande. La codification des couleurs est maintenue pour faciliter la compréhension (rappelez-vous, les couleurs plus claires sont moins probables ; les couleurs plus denses sont plus probables). Dans cet exemple, la valeur de demande la plus probable est de 167 unités (+/-), c’est pourquoi le point blanc dans la plage de valeurs recadrée de la Figure 6 est positionné directement au-dessus de la barre la plus haute de l’histogramme. Cependant, nous attribuons également des probabilités de demande à des valeurs de demande extrêmement faibles et élevées (environ 80 et 260 unités, respectivement, toutes deux de couleur orange très clair). Cela démontre la richesse potentielle des données d’une prévision probabiliste, et des histogrammes similaires sont inclus dans la feuille de calcul Excel - un pour chacun de nos SKUs (voir la Figure 4). En utilisant ces histogrammes (comme dans la Figure 7 ci-dessus), les valeurs de demande (en unités) ayant une probabilité non nulle d’occurrence peuvent être identifiées et prises en compte dans le PIR.

2.1 La construction d’une prévision probabiliste

Bien qu’il soit possible de construire une prévision probabiliste réelle à partir de données historiques dans Excel, il est sans doute l’outil le moins adapté à cette fin. Dans l’ensemble, les détails de la construction d’une prévision probabiliste de qualité de production dépassent le cadre de ce document, c’est pourquoi des prévisions probabilistes synthétiques ont été sélectionnées pour des raisons de simplicité. Les paramètres de ces prévisions synthétiques peuvent être manipulés dans les générateurs de distribution (voir Figure 4). Il est cependant recommandé d’étudier d’abord les paramètres par défaut avant d’apporter des ajustements.

Dans les pratiques courantes de la supply chain, la demande est généralement considérée comme étant normalement distribuée, mais cela est rare. Dans les chaînes d’approvisionnement réelles, la plupart des SKUs s’écartent des modèles de distribution normale. Compte tenu de cette réalité, nous avons délibérément sélectionné trois modèles de distribution différents : normal (pour les claviers), binomiale négative (pour les stylos) et bimodale (pour les bibliothèques - un mélange de deux modèles de distribution binomiale négative). Les justifications de cette hypothèse sont les suivantes.

Par exemple, nous supposons que les bibliothèques sont achetées à la fois par des particuliers et des entreprises (par exemple, des écoles), c’est pourquoi nous utilisons une distribution bimodale. Dans le paramétrage par défaut des bibliothèques, il y a une demande fréquente de la part des particuliers, avec un ou deux exemplaires achetés par client. Cela représente le premier mode de la distribution (voir Figure 4). Les entreprises, en revanche, représentent des sources de demande moins fréquentes mais passent des commandes plus importantes (plus importantes que celles des particuliers). Lorsque cela se produit, leur demande est ajoutée à la demande générée par les achats des particuliers, et le deuxième mode de la distribution apparaît. Ce deuxième mode est décalé vers la droite (représentant des valeurs de demande élevées) et est nettement plus petit que le premier mode, ce qui reflète le fait qu’il se produit moins fréquemment (Figure 4). Notre modèle suppose également que les stylos sont achetés par des particuliers avec une demande occasionnellement élevée (par exemple, les étudiants achètent avant les dates d’examens scolaires). Enfin, pour refléter le fait qu’une distribution normale se produit occasionnellement, les ventes de claviers suivent un modèle de distribution normale.

Dans les générateurs de distribution (Figure 4), on peut modifier les distributions de demande en modifiant les paramètres dans les cellules manipulables. Par exemple, augmenter la moyenne des claviers (voir “paramètres NORM” dans la Figure 4) de 40 à 50 entraînera un décalage de 10 unités vers la droite de la distribution. En raison de cette augmentation de la demande moyenne, le retour sur investissement attendu pour toutes les unités de clavier augmentera. De même, on peut apporter des modifications aux paramètres des distributions binomiale négative (stylos) et bimodale (bibliothèques).

Comme Excel ne permet pas ce type de calcul, cette démonstration limite les modifications à 100 unités par produit. Par exemple, si la moyenne des claviers est fixée à 99, près de 50% des unités de demande ne pourront pas être calculées dans la feuille de calcul des décisions d’achat micro.

2.2 Sélection d’une horizon pour une prévision probabiliste de la demande

En général, les prévisions sont divisées en intervalles quotidiens/hebdomadaires/mensuels, bien que ces périodes discrètes aient une utilité et une valeur limitées du point de vue de l’approvisionnement. La demande au cours des délais d’approvisionnement à venir ne peut pas être couverte par les décisions d’achat prises aujourd’hui, à moins d’autoriser les commandes en souffrance, car les unités achetées arriveront après une période égale au délai d’approvisionnement. Ainsi, la demande doit être couverte avec le stock disponible en magasin et le stock en commande (voir Figure 8), en supposant que les unités en commande arrivent avant la demande. Par conséquent, la prévision probabiliste concerne la demande entre les points de commande ou, en d’autres termes, la demande pendant la période de commande 1 (voir Figure 9). La demande future plus éloignée sera couverte par les commandes futures (voir période de commande 2, dans la Figure 9).

Figure 8. Stock disponible (colonne F) et Stock en commande (colonne G), mis en évidence en rouge, se trouvent dans décisions d'achat micro. Le délai d'approvisionnement, colonne I, est mis en évidence en bleu.

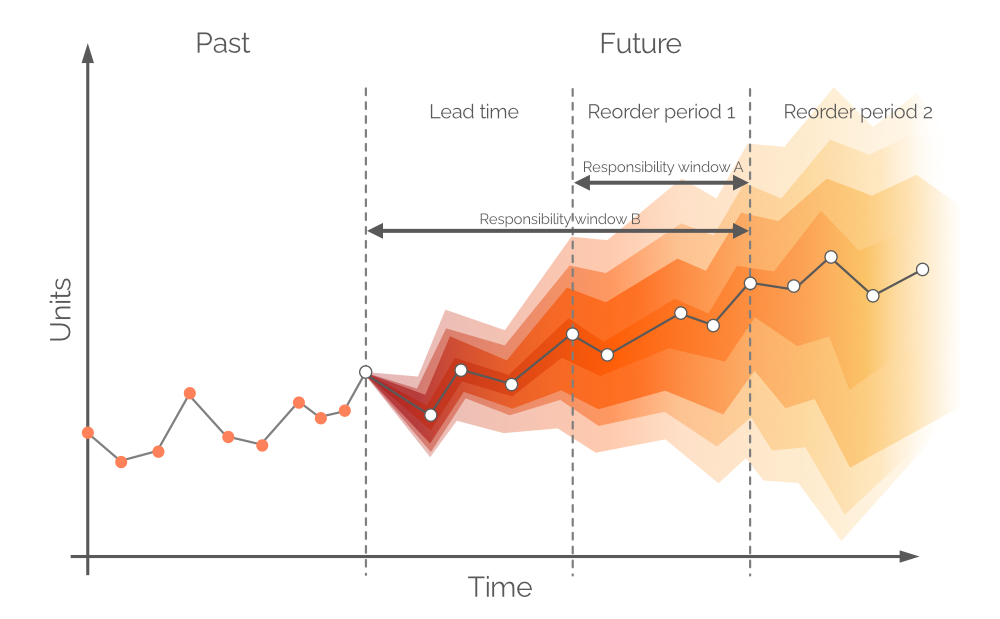
Figure 9. Une représentation visuelle des fenêtres de responsabilité alternatives. La demande est sur l'axe des y, le temps sur l'axe des x, avec la ligne verticale grise en pointillés à gauche indiquant le moment actuel ("maintenant", selon la Figure 6). La prévision probabiliste dans ce document concerne la demande sur l'horizon égal à Fenêtre de responsabilité B.

En théorie, la prévision probabiliste de la demande devrait être construite sur la période de temps équivalente à la Période de réapprovisionnement 1 - cette fenêtre de temps est appelée Fenêtre de responsabilité A (voir Figure 9). Pour ce faire, nous aurions besoin de faire des projections futures pour les stocks disponibles et les stocks en commande à la fin du délai de livraison. Cependant, la demande pendant le délai de livraison - pour laquelle nous avons déjà pris des décisions lors de la période de commande précédente - est également probabiliste, et cela entraînerait des niveaux de stock qui sont eux-mêmes des distributions de probabilité³. En autorisant les commandes en attente (une pratique courante dans certains secteurs), une prévision probabiliste peut être construite sur une période conjointe (délai de livraison plus période de réapprovisionnement 1, selon la Figure 9, également appelée Fenêtre de responsabilité B).

On peut supposer que les niveaux actuels de stock disponible et de stock en commande serviront à satisfaire la demande pendant la période de délai de livraison. En cas de rupture de stock, toute demande ultérieure sera couverte par des commandes en attente. Ces commandes en attente seront satisfaites par les décisions d’achat prises à partir d’aujourd’hui. Cela nous permet de traiter les stocks disponibles et les stocks en commande comme des valeurs discrètes (au lieu de valeurs aléatoires)⁴.

3. Identification des options de décision de réapprovisionnement réalisables

Dans un scénario réel de réapprovisionnement des stocks, il serait nécessaire de définir toutes les options de décision réalisables, car il n’y a pas de moyen direct de passer d’une prévision probabiliste à la meilleure décision unique (quantité d’achat, dans ce cas) pour chaque produit. Au lieu d’un choix unique et parfait, une approche probabiliste présente une gamme de décisions possibles que l’on doit prendre en compte en termes de faisabilité.

Faisabilité ici a le sens courant qu’une décision est immédiatement réalisable ; elle peut être exécutée “telle quelle” sans calculs ou vérifications supplémentaires. Par exemple, une décision est “réalisable” si elle est rentable et satisfait toutes nos contraintes (par exemple, les MOQs, les EOQs, les tailles de lot, les expéditions de conteneurs complètes, et toute autre contrainte qui peut exister dans notre supply chain)⁵.

À chaque ligne de la feuille de décisions d’achat micro (Figures 3 et 10), nous devons envisager d’ajouter une unité de stock supplémentaire à notre commande d’achat pour un produit particulier⁶. Notre “présent” (ou jour 1 de cette expérience) commence à la ligne 29, qui montre le niveau de stock actuel. Celui-ci est calculé comme la somme du stock disponible et du stock en commande. Si nous décidons d’ajouter une unité à la commande d’achat, la quantité totale d’achat sera calculée dans la colonne L comme la somme de toutes les unités considérées jusqu’à présent pour l’achat (voir les notes dans la Figure 10).

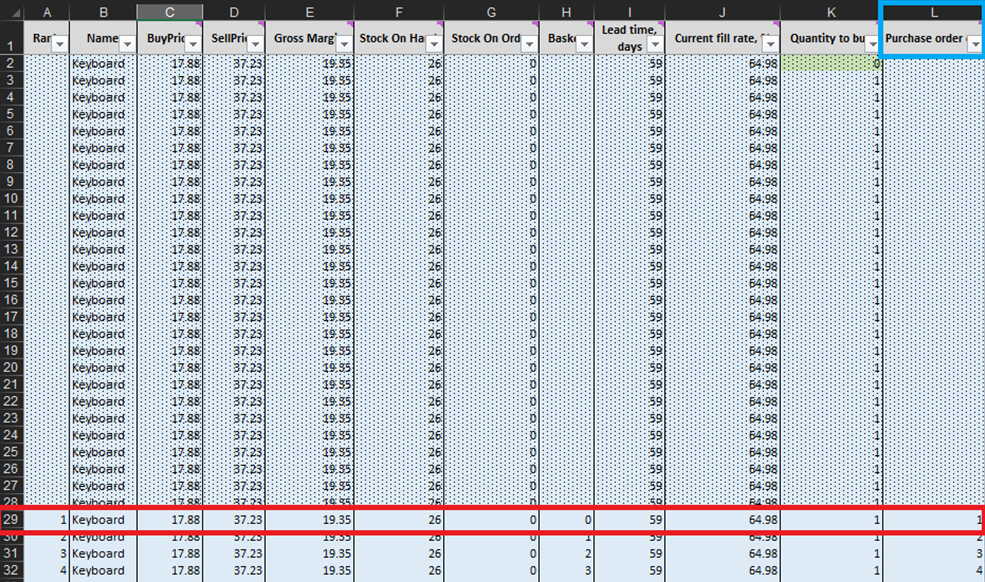
Figure 10. Vue depuis la feuille de décision d'achat micro. La ligne 29, mise en évidence en rouge, est le point de départ de notre expérience (pour les claviers). La colonne de commande d'achat est mise en évidence en bleu. Le même principe s'applique aux lignes 140 (pour les commandes de stylos) et 240 (pour les commandes de bibliothèques).

Une fois ces décisions d’inventaire réalisables identifiées, nous calculerons et classerons la récompense économique de chaque achat possible. Notez que nous n’évaluons pas la récompense d’achat pour les unités qui sont actuellement soit en stock soit en commande (colonnes F et G dans la Figure 10). Étant donné que nous avons déjà acheté ces unités, la récompense économique théorique a été déterminée (et classée) à une date antérieure. Par exemple, si nous examinons les données des claviers dans la Figure 10, il y a actuellement 26 unités en stock. Ainsi, nous commencerons les calculs à la ligne 29 et nous demanderons si nous devons commander notre première unité de stock supplémentaire (ce qui porterait le niveau de stock de 26 à 27 unités).

3.1 Évaluation des décisions d’achat réalisables

Afin de choisir la meilleure quantité d’achat pour chaque produit, il est nécessaire de calculer le retour monétaire attendu au niveau de l’unité pour chaque quantité réalisable pour chaque produit (en tenant compte de l’avenir incertain représenté par la prévision probabiliste). Il s’agit d’un concept de valeur attendue adapté au niveau le plus granulaire de la gestion des stocks décisionnelle.

En réalité, tous les types de facteurs économiques doivent être pris en compte lors de la tentative de calcul du retour attendu pour chaque décision réalisable⁷. Aux fins de cette démonstration, voici les facteurs que nous prendrons en compte :

Prix de vente : le montant que nous facturons aux clients pour le produit.
Coût de stockage : le coût pour nous de détenir le produit.
Prix d’achat : le montant que cela nous coûte d’acheter le produit auprès de notre fournisseur/grossiste.
Couverture de rupture de stock : expliquée en détail ci-dessous car il s’agit d’un facteur moins connu mais néanmoins important⁸.

Figure 11. Note explicative pour le prix d'achat, visible en survolant l'en-tête de colonne. Il y a une définition pour chaque colonne dans chaque feuille du document Excel.

La couverture de rupture de stock représente une incitation financière à garder une unité d’un produit en stock, mais pas dans le but explicite de le vendre. Ce facteur économique est utilisé pour modéliser l’importance relative d’un produit par rapport aux autres. Il incite à éviter une rupture de stock pour les produits qui pourraient être considérés comme moins importants en raison de leurs contributions marginales directes, car ces produits peuvent contribuer de manière significative aux marges bénéficiaires de manière indirecte. En tant que tel, il est plus semblable à un facteur de récompense⁹. Bien que ce facteur soit flou, il est crucial d’identifier tous les produits critiques (même ceux qui ne sont pas des contributeurs marginaux directs).

3.2 Calcul du score de chaque décision réalisable

La conséquence économique totale (ou récompense d’achat) d’une décision de réapprovisionnement des stocks est la somme de tous les facteurs économiques, y compris la marge attendue, le coût d’inventaire attendu et la couverture de rupture de stock (définis en détail ci-dessous). Le coût de stockage est inclus dans ces calculs en tant que facteur négatif, agissant comme une force opposée pour équilibrer nos décisions de réapprovisionnement des stocks.

Voici une analyse des implications économiques des formules dans chaque colonne, en utilisant la ligne 29 de la feuille Micro purchasing decisions comme exemple (voir Figure 12).

Figure 12. Une ventilation des facteurs par colonnes clés, en utilisant la ligne 29 de Micro purchasing decisions (feuille Excel 2). Certaines colonnes ont été masquées pour la commodité de la figure.

Pour calculer la récompense attendue pour chaque décision, nous avons besoin des facteurs suivants :

Marge brute (colonne E) = Prix de vente - Prix d’achat.

Probabilité de vente (colonne Q) = vérifier la formule dans la feuille¹⁰.

Probabilité de non-vente (pas de colonne) = 100% - Probabilité de vente

Marge attendue (colonne R) = Marge brute * Probabilité de vente/100.

Facteur d’agressivité (colonne S) = Varie de 0 à 1. 0,8 sélectionné pour cet outil.

Couverture de rupture de stock (colonne T) = Prix de vente * Facteur d’agressivité * Probabilité de vente

Coût de stockage (colonne U)

Coût attendu des stocks (colonne V) = Coût de stockage * Probabilité de non-vente¹¹.

En utilisant les données ci-dessus, la récompense d’achat pour chaque décision de stockage au niveau micro (chaque unité de chaque produit) est calculée comme suit :

Récompense d’achat (colonne W) = Marge attendue + Couverture de rupture de stock + Coût attendu des stocks.

Une fois que nous avons estimé la récompense d’achat, nous pouvons calculer le score final que nous utiliserons ensuite pour classer toutes les décisions envisagées.

Score (colonne Y) = Récompense d’achat / Investissement (colonne X)¹².

Étant donné que la couverture de rupture de stock est un facteur flou qui intègre à la fois les rendements directs et indirects, la récompense d’achat ne reflète pas strictement le rendement attendu d’une décision de stockage isolée. Si l’on souhaite calculer ce type de rendement, on exclurait la couverture de rupture de stock de cette formule¹³.

4. Classement des décisions de réapprovisionnement des stocks réalisables

Une fois que nous avons le score pour chaque décision d’achat de stock réalisable (pour chaque produit), une liste est générée et triée par ordre décroissant (du plus élevé au plus bas) dans Décisions d’achat classées (voir Figure 13). Chaque décision de stock réalisable est triée en termes de pourcentage de retour sur investissement positif. Un classement ordinal (1er, 2e, 3e, etc.) est également attribué à chaque décision (voir colonne A dans la même figure).

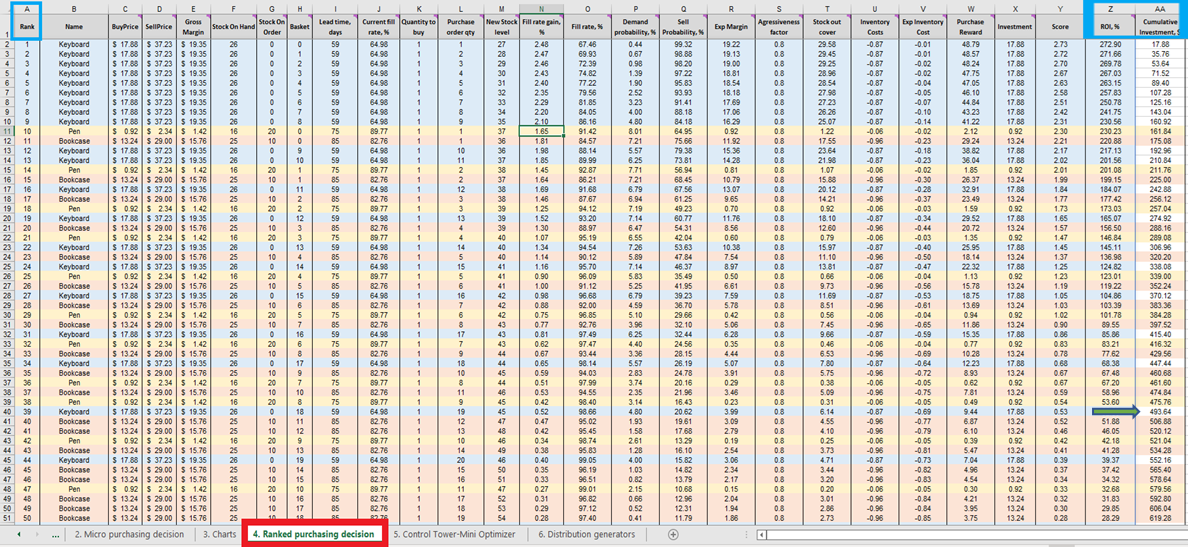
Figure 13. Emplacement des décisions d'achat classées en rouge. Les colonnes A, Z et AA sont surlignées en bleu. La cellule 40 (le point de coupure pour un budget de 500 $ - la valeur par défaut de la feuille de calcul) est indiquée par la flèche verte.

Décisions d’achat classées présente des lignes codées par couleur pour chaque produit (claviers, stylos et bibliothèques), utilisées ici pour démontrer comment le choix d’ajouter une seule unité supplémentaire de n’importe quel produit donné interagit avec chaque autre unité supplémentaire de chaque autre produit. Chacune de ces décisions de stockage influence collectivement le retour sur investissement. Enfin, une valeur d’investissement cumulatif est calculée (colonne AA, Figure 13). Cela peut être utilisé pour indiquer où il convient de mettre fin aux décisions d’achat compte tenu des contraintes budgétaires - bien que ce ne soit qu’un indicateur de fin possible¹⁴.

5. Détermination des critères de fin

En ce qui concerne la sélection d’un point de fin (à la fois dans les Décisions d’achat classées et dans la réalité), les critères varieront en fonction d’un ensemble de variables. Par exemple, on peut avoir un budget modeste et donc maximiser le retour sur investissement pose problème compte tenu de marges particulièrement serrées. Alternativement, il est possible d’avoir un objectif global de taux de service et il faut alors équilibrer cette priorité avec une volonté de maximiser les marges bénéficiaires.

Pour être encore plus précis, les critères de fin peuvent englober une volonté de maximiser le retour sur investissement avec des objectifs de taux de service variables pour chaque produit ou catégorie. Les critères de fin sont donc un choix stratégique qui doit être fait après une réflexion franche sur les objectifs commerciaux globaux d’une entreprise. La reconstitution des stocks priorisée (PIR) est remarquablement flexible à cet égard ; les critères de fin pour chaque cycle d’achat peuvent être ajustés en utilisant la même procédure de classement globale.

Pour des visualisations explicites de nos décisions de reconstitution des stocks possibles, il existe trois graphiques pour chaque produit dans le tableau de bord Charts (feuille 3, voir Figure 14). D’un intérêt particulier est “Forces motrices_nom du produit” (l’exemple du clavier est utilisé dans la Figure 14), qui montre l’évolution du retour sur investissement en fonction de différentes quantités d’achat au niveau de l’unité.

Comme le montre le graphique, il y a un point où des quantités d’achat accrues entraîneront un retour sur investissement négatif. Cela est dû au fait qu’à un certain niveau, il est inutile d’acheter plus d’unités car nos marges attendues seront considérablement réduites par des coûts d’inventaire attendus plus élevés.

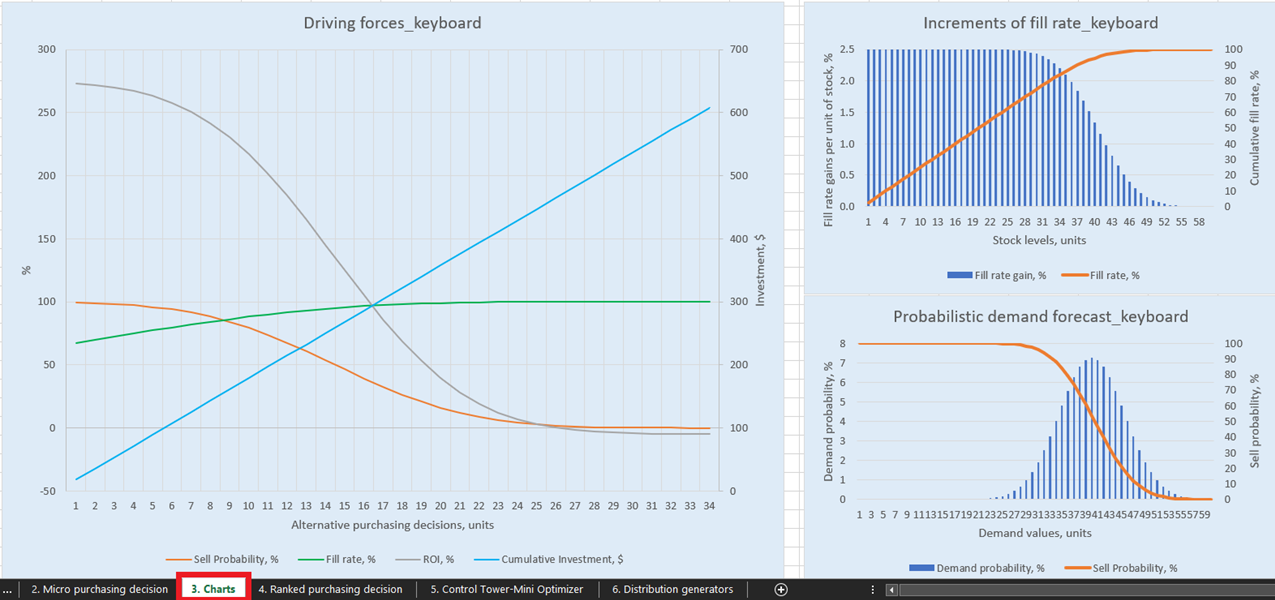
Figure 14. Vue des "Forces motrices_clavier" dans Charts, emplacement surligné en rouge.

Une fois les critères de fin déterminés, les décisions de reconstitution des stocks prioritaires sont agrégées par SKU, ce qui met à jour la Quantité, l’Investissement et le Taux de remplissage attendu atteint dans Output-Purchase Recommendation pour chaque SKU (voir Figure 15). On peut modifier les contraintes budgétaires (de 0 $ à 1450 $), ce qui mettra à jour la liste d’achat recommandée. Pour plus de commodité, la tour de contrôle comprend deux blocs supplémentaires : Cas de base - copie papier et Modifications apportées au scénario de base. Le premier est statique et affiche les paramètres par défaut de la démonstration tels que conçus par Lokad ; le second affiche la différence entre les modifications apportées et les paramètres par défaut de Lokad.

La liste de recommandation d’achat dans la tour de contrôle représente l’objectif de cette démonstration (voir Figure 15).

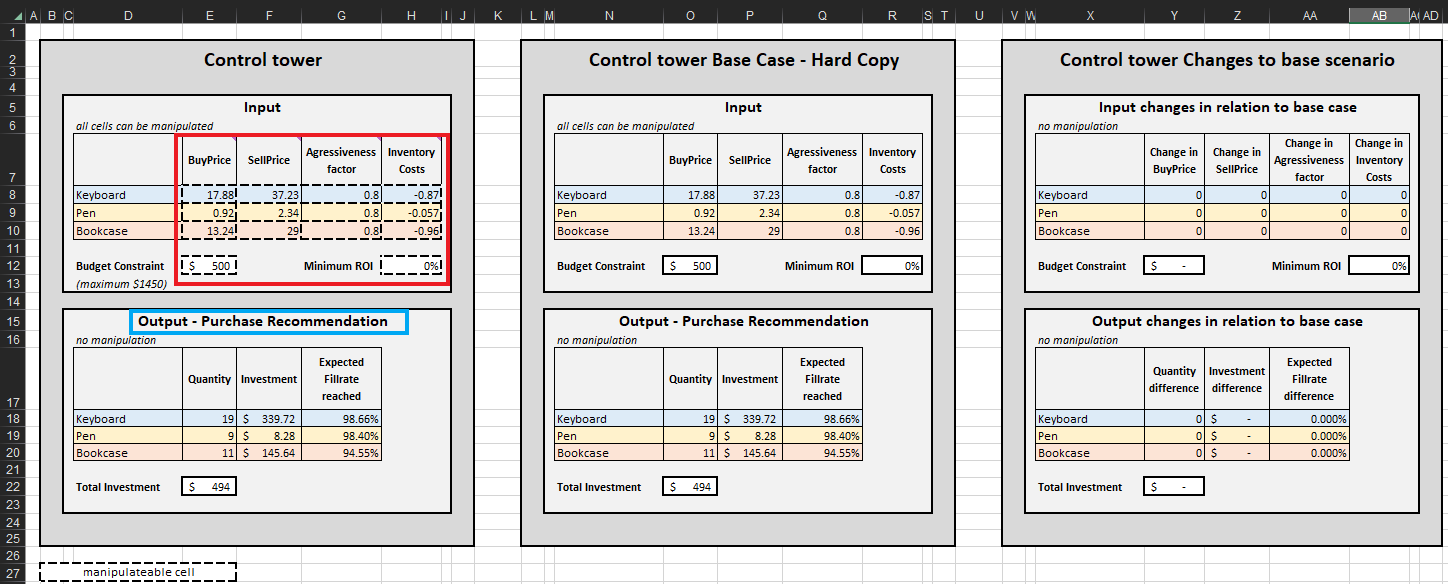
Figure 15. Vue de la tour de contrôle - Mini Optimizer (feuille 5). Les cellules manipulables sont surlignées en rouge. "Recommandation d'achat" est surligné en bleu et représente l'objectif d'une approche de reconstitution des stocks prioritaires.

6. Conclusion

Les prévisions traditionnelles des séries temporelles sont tout simplement incapables de capturer le niveau de granularité nécessaire pour prendre des décisions de reconstitution des stocks qui reflètent l’incertitude future et l’ampleur totale des contraintes et des moteurs. Cela est dû à l’absence d’une dimension d’incertitude explicite, représentée par des valeurs de probabilité pour les résultats futurs attendus. Comme une série temporelle traditionnelle est effectivement aveugle à ce type de données, une méthode classique de gestion des stocks telle que le stock de sécurité relève de la conjecture ; si on en a trop peu, on perd des ventes rentables avec un ROI attendu positif ; si on en a trop, on réduit son ROI en stockant des unités qui (comme le montre la feuille de calcul) ont un ROI attendu négatif.

La reconstitution des stocks prioritaires, en utilisant des prévisions probabilistes, est notre solution à ce problème. Une telle approche considère les choix de reconstitution des stocks en combinaison, plutôt qu’isolément. Ce faisant, la récompense financière attendue de nos choix de reconstitution des stocks peut être entièrement quantifiée et révélée. La base d’une telle approche consiste à embrasser l’incertitude et à exploiter les prévisions probabilistes. À son tour, on peut également obtenir une meilleure compréhension des niveaux de service (par SKU) qui génèrent des récompenses financières significatives, plutôt que de fixer des objectifs arbitraires.

L’approche de reconstitution des stocks prioritaires présentée dans ce document a été construite à l’aide de données synthétiques et de paramètres étroits. Ces choix ont été faits pour adapter un outil courant (Excel) à un objectif inhabituel (PIR). Parmi les autres concessions nécessaires, les SKU et les unités ont été limités (respectivement à 3 et 100) pour réduire le temps de traitement, car l’ensemble des données d’un catalogue (sans parler des données de plusieurs magasins) serait trop laborieux à traiter. De plus, aucune contrainte de chaîne d’approvisionnement n’a été ajoutée. De manière cruciale, Excel n’est pas conçu pour traiter des variables aléatoires - une étape clé dans la génération de prévisions probabilistes et de politiques PIR. Ces limitations ne s’appliquent pas à une solution PIR de qualité de production.

Les praticiens de la chaîne d’approvisionnement dont les entreprises ont dépassé Excel sont invités à envoyer un e-mail à contact@lokad.com pour organiser une démonstration d’une solution PIR de qualité de production.

7. Aperçu de la feuille de calcul

7.1 Lisez-moi

Cette feuille sert de page d’accueil pour l’utilisateur. Il y a un lien vers un tutoriel en ligne (celui que vous êtes en train de lire).

7.2 Micro-décisions d’achat

Il s’agit de la deuxième feuille et elle est consacrée à l’analyse financière fine et granulaire de toutes les options de décision de réapprovisionnement réalisables. Veuillez noter qu’aucune manipulation manuelle des données n’est effectuée ici. Cette feuille affiche uniquement les résultats des calculs basés sur les entrées des feuilles “Control Tower” et “Distribution generators”.