Généralisation (Prévision)
La généralisation est la capacité d’un algorithme à générer un modèle - en exploitant un ensemble de données - qui fonctionne bien sur des données non vues auparavant. La généralisation est d’une importance capitale pour la supply chain, car la plupart des décisions reflètent une anticipation de l’avenir. Dans le contexte de la prévision, les données sont invisibles car le modèle prédit des événements futurs, qui sont non observables. Bien que des progrès substantiels, tant théoriques que pratiques, aient été réalisés sur le front de la généralisation depuis les années 1990, la généralisation véritable reste insaisissable. La résolution complète du problème de généralisation ne serait pas très différente de celle du problème de l’intelligence générale artificielle. De plus, la supply chain ajoute son lot de problèmes épineux aux défis de généralisation courants.

Aperçu d’un paradoxe
Créer un modèle qui fonctionne parfaitement sur les données dont on dispose est simple : il suffit de mémoriser intégralement l’ensemble de données, puis d’utiliser cet ensemble de données lui-même pour répondre à toute requête concernant l’ensemble de données. Comme les ordinateurs sont bons pour enregistrer de grands ensembles de données, il est facile de concevoir un tel modèle. Cependant, cela est généralement inutile1, car l’intérêt d’un modèle réside dans sa capacité prédictive au-delà de ce qui a déjà été observé.
Un paradoxe apparemment inéluctable se présente : un bon modèle est celui qui fonctionne bien sur des données qui ne sont actuellement pas disponibles mais, par définition, si les données ne sont pas disponibles, l’observateur ne peut pas effectuer l’évaluation. Le terme “généralisation” fait donc référence à la capacité insaisissable de certains modèles à conserver leur pertinence et leur qualité au-delà des observations disponibles au moment de la construction du modèle.
Bien que la mémorisation des observations puisse être rejetée comme une stratégie de modélisation inadéquate, toute stratégie alternative de création d’un modèle est potentiellement sujette au même problème. Peu importe à quel point le modèle semble bien fonctionner sur les données actuellement disponibles, il est toujours concevable que cela soit simplement une question de chance, ou pire, un défaut de la stratégie de modélisation. Ce qui peut, à première vue, apparaître comme un paradoxe statistique marginal est en réalité un problème de grande envergure.
À titre d’exemple, en 1979, la SEC (Securities and Exchange Commission), l’agence américaine chargée de réglementer les marchés financiers, a introduit sa célèbre Règle 156. Cette règle oblige les gestionnaires de fonds à informer les investisseurs que les performances passées ne sont pas indicatives des résultats futurs. Les performances passées sont implicitement le “modèle” que la SEC met en garde contre le fait de ne pas faire confiance à sa puissance de “généralisation” ; c’est-à-dire sa capacité à dire quelque chose sur l’avenir.
Même la science elle-même a du mal à extrapoler la “vérité” en dehors d’un ensemble restreint d’observations. Les scandales de “mauvaise science”, qui ont éclaté dans les années 2000 et 2010 autour du p-hacking, indiquent que des domaines entiers de recherche sont défaillants et ne peuvent pas être fiables2. Alors qu’il existe des cas de fraude flagrante où les données expérimentales ont été clairement falsifiées, la plupart du temps, le cœur du problème réside dans les modèles ; c’est-à-dire dans le processus intellectuel utilisé pour généraliser ce qui a été observé.
Sous son aspect le plus vaste, le problème de généralisation est indissociable de celui de la science elle-même, il est donc aussi difficile que de reproduire l’étendue de l’ingéniosité et du potentiel humains. Cependant, la version statistique plus étroite du problème de généralisation est beaucoup plus abordable, et c’est cette perspective qui sera adoptée dans les sections à venir.
Émergence d’une nouvelle science
La généralisation est apparue comme un paradigme statistique au tournant du XXe siècle, principalement à travers le prisme de la précision des prévisions3, qui représente un cas particulier étroitement lié aux prévisions des séries temporelles. Au début des années 1900, l’émergence d’une classe moyenne possédant des actions aux États-Unis a suscité un intérêt massif pour des méthodes qui aideraient les gens à obtenir des rendements financiers sur leurs actifs échangés. Les diseurs de bonne aventure et les prévisionnistes économiques se sont tous deux efforcés d’extrapoler les événements futurs pour un public avide de payer. Des fortunes ont été faites et perdues, mais ces efforts ont très peu éclairé la “bonne” façon d’aborder le problème.
La généralisation est restée, dans l’ensemble, un problème déconcertant pendant la majeure partie du XXe siècle. Il n’était même pas clair si cela relevait du domaine des sciences naturelles, régies par les observations et les expérimentations, ou du domaine de la philosophie et des mathématiques, régies par la logique et la cohérence interne.
L’espace a continué à avancer jusqu’à un moment décisif en 1982, l’année de la première compétition de prévision publique - connue sous le nom de compétition M4. Le principe était simple : publier un ensemble de données de 1000 séries temporelles tronquées, laisser les concurrents soumettre leurs prévisions, puis publier le reste de l’ensemble de données (les queues tronquées) ainsi que les précisions respectives obtenues par les participants. Grâce à cette compétition, la généralisation, toujours perçue à travers le prisme de la précision des prévisions, était entrée dans le domaine des sciences naturelles. Par la suite, les compétitions de prévision sont devenues de plus en plus fréquentes.
Quelques décennies plus tard, Kaggle, fondé en 2010, a ajouté une nouvelle dimension à de telles compétitions en créant une plateforme dédiée aux problèmes de prédiction générale (pas seulement des séries temporelles). En février 20235, la plateforme a organisé 349 compétitions avec des prix en argent. Le principe reste le même que celui de la compétition M originale : un ensemble de données tronquées est mis à disposition, les concurrents soumettent leurs réponses aux tâches de prédiction données, et enfin, les classements ainsi que la partie cachée de l’ensemble de données sont révélés. Les compétitions sont toujours considérées comme la référence pour l’évaluation correcte de l’erreur de généralisation des modèles.
Problèmes de surapprentissage et de sous-apprentissage
Le surapprentissage, comme son antonyme le sous-apprentissage, est un problème qui se pose fréquemment lors de la création d’un modèle basé sur un ensemble de données donné, et qui compromet le pouvoir de généralisation du modèle. Historiquement6, le surapprentissage est apparu comme le premier obstacle bien compris à la généralisation.
La visualisation du surapprentissage peut être réalisée à l’aide d’un problème de modélisation de séries temporelles simple. Dans le cadre de cet exemple, supposons que l’objectif soit de créer un modèle qui reflète une série d’observations historiques. L’une des options les plus simples pour modéliser ces observations est un modèle linéaire, comme illustré ci-dessous (voir Figure 1).
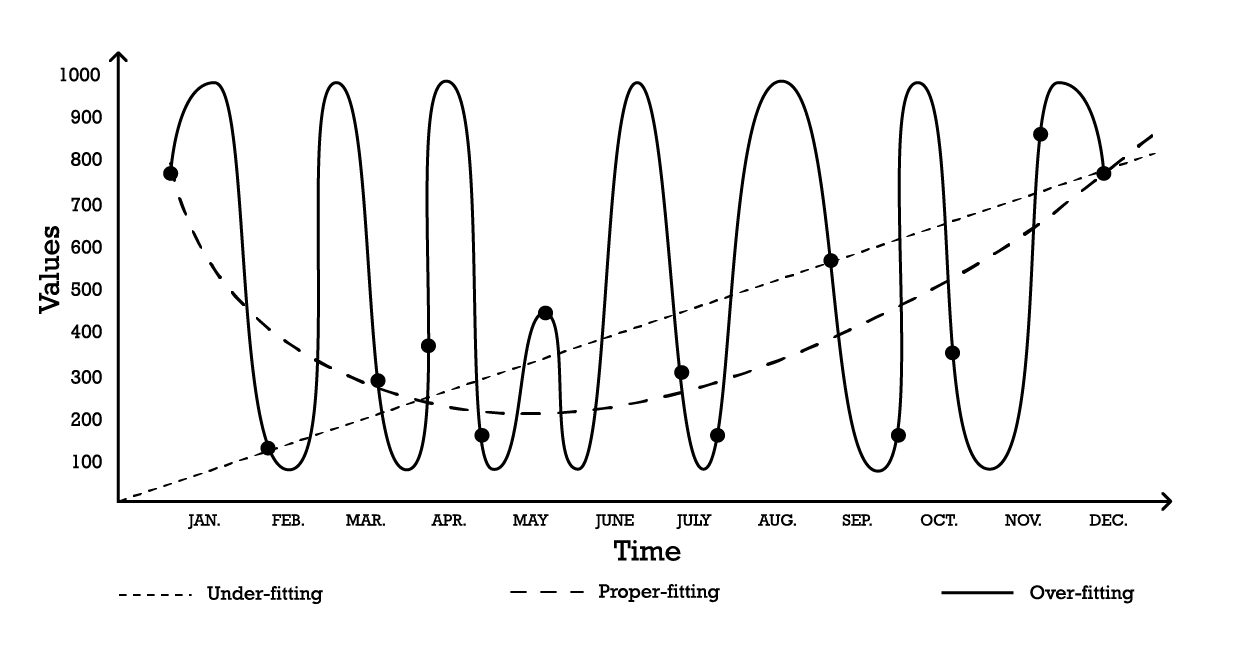
Figure 1 : Un graphique composite représentant trois tentatives différentes de « fitting » une série d'observations.
Avec deux paramètres, le modèle de “sous-apprentissage” est robuste, mais il, comme son nom l’indique, sous-apprend les données, car il échoue clairement à capturer la forme globale de la distribution des observations. Cette approche linéaire a un biais élevé mais une faible variance. Dans ce contexte, le biais doit être compris comme la limitation inhérente de la stratégie de modélisation à capturer les détails des observations, tandis que la variance doit être comprise comme la sensibilité aux petites fluctuations - éventuellement du bruit - des observations.
Un modèle assez complexe pourrait être adopté, comme la courbe de “surapprentissage” (Figure 1). Ce modèle comprend de nombreux paramètres et s’ajuste exactement aux observations. Cette approche a un biais faible mais une variance démontrablement élevée. Alternativement, un modèle d’une complexité intermédiaire pourrait être adopté, comme on le voit dans la courbe de “bon ajustement” (Figure 1). Ce modèle comprend trois paramètres, a un biais moyen et une variance moyenne. Parmi ces trois options, le modèle de bon ajustement est invariablement celui qui se comporte le mieux en termes de généralisation.
Ces options de modélisation représentent l’essence du compromis biais-variance.7 8 Le compromis biais-variance est un principe général qui stipule que le biais peut être réduit en augmentant la variance. L’erreur de généralisation est minimisée en trouvant le bon équilibre entre la quantité de biais et de variance.
Historiquement, du début du XXe siècle jusqu’au début des années 2010, un modèle surajusté était défini9 comme un modèle contenant plus de paramètres que ce qui peut être justifié par les données. En effet, à première vue, ajouter trop de degrés de liberté à un modèle semble être la recette parfaite pour des problèmes de surapprentissage. Pourtant, l’émergence du deep learning a prouvé que cette intuition, ainsi que la définition du surapprentissage, étaient trompeuses. Ce point sera réexaminé dans la section sur le double-descente profonde.
Validation croisée et backtesting
La validation croisée est une technique de validation de modèle utilisée pour évaluer dans quelle mesure un modèle généralisera au-delà de son ensemble de données de support. Il s’agit d’une méthode de sous-échantillonnage qui utilise différentes parties des données pour tester et entraîner respectivement un modèle lors de différentes itérations. La validation croisée est le fondement des pratiques modernes de prédiction, et presque tous les participants gagnants des compétitions de prédiction utilisent largement la validation croisée.
De nombreuses variantes de la validation croisée existent. La variante la plus populaire est la validation k-fold où l’échantillon d’origine est divisé de manière aléatoire en k sous-échantillons. Chaque sous-échantillon est utilisé une fois comme données de validation, tandis que le reste - tous les autres sous-échantillons - est utilisé comme données d’entraînement.
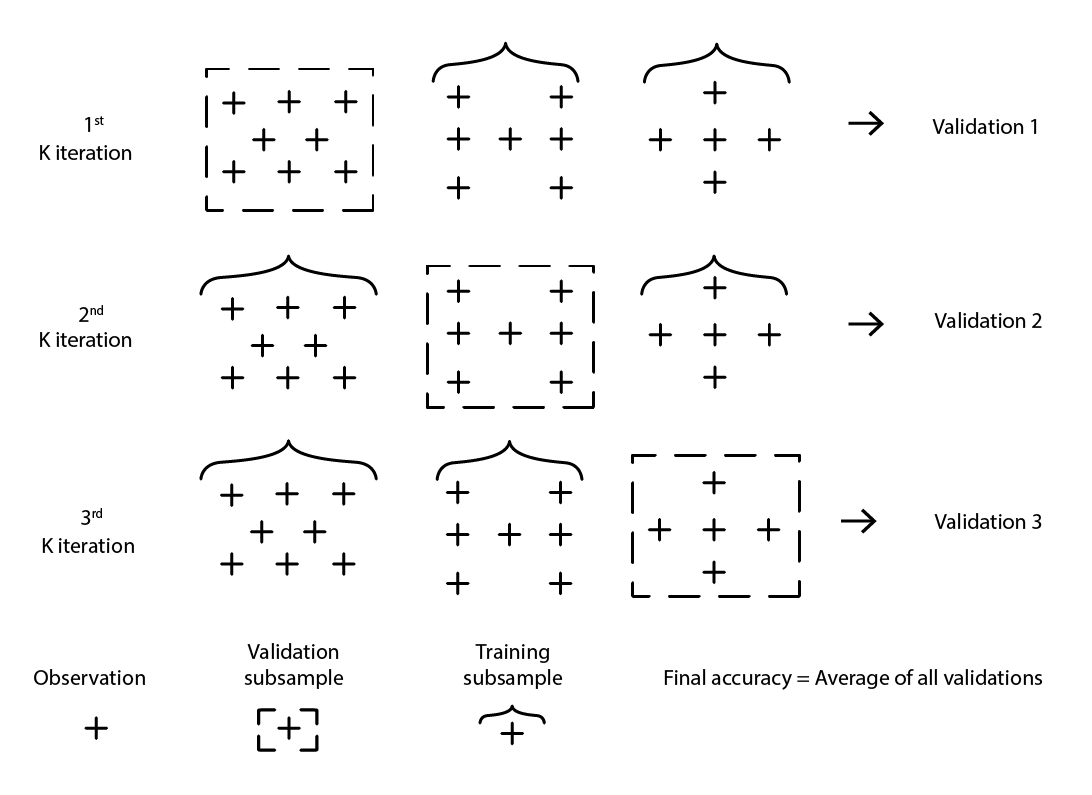
Figure 2 : Un exemple de validation k-fold. Les observations ci-dessus proviennent toutes du même ensemble de données. La technique construit donc des sous-échantillons de données à des fins de validation et d'entraînement.
Le choix de la valeur k, le nombre de sous-échantillons, est un compromis entre les gains statistiques marginaux et les exigences en termes de ressources informatiques. En effet, avec la validation k-fold, les ressources informatiques augmentent linéairement avec la valeur k, tandis que les avantages, en termes de réduction de l’erreur, connaissent des rendements décroissants extrêmes10. En pratique, choisir une valeur de 10 ou 20 pour k est généralement “suffisant”, car les gains statistiques associés à des valeurs plus élevées ne justifient pas les inconvénients supplémentaires liés à une plus grande dépense de ressources informatiques.
La validation croisée suppose que l’ensemble de données peut être décomposé en une série d’observations indépendantes. Cependant, dans la supply chain, ce n’est généralement pas le cas, car l’ensemble de données reflète généralement une sorte de données historisées où une dépendance temporelle est présente. En présence de temps, le sous-échantillon d’entraînement doit être strictement “antérieur” au sous-échantillon de validation. En d’autres termes, le “futur”, par rapport à la coupure de rééchantillonnage, ne doit pas fuiter dans le sous-échantillon de validation.
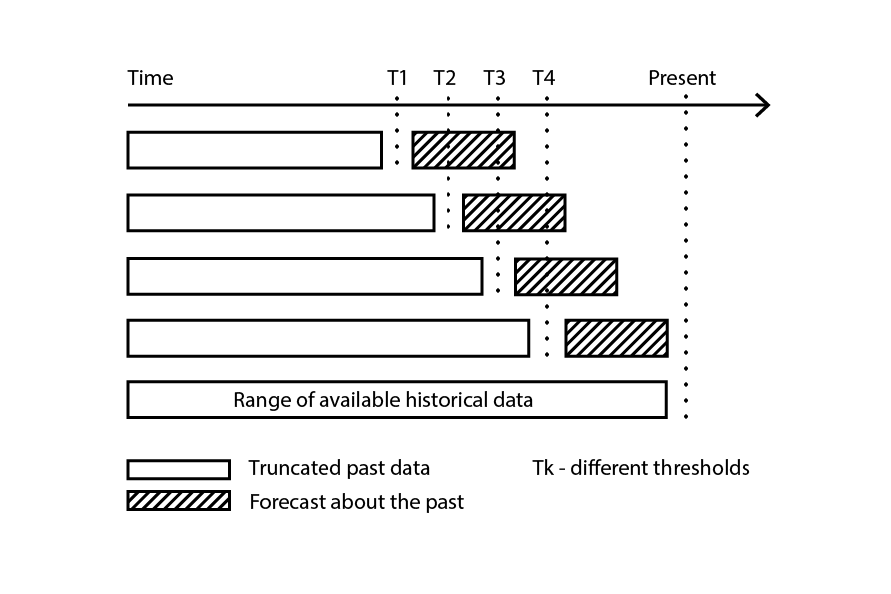
Figure 3 : Un exemple de processus de backtesting construit des sous-échantillons de données à des fins de validation et d'entraînement.
Le backtesting représente la variante de la validation croisée qui aborde directement la dépendance temporelle. Au lieu de considérer des sous-échantillons aléatoires, les données d’entraînement et de validation sont respectivement obtenues par une coupure : les observations antérieures à la coupure appartiennent aux données d’entraînement, tandis que les observations postérieures à la coupure appartiennent aux données de validation. Le processus est répété en choisissant une série de valeurs de coupure distinctes.
La méthode de rééchantillonnage qui est au cœur de la validation croisée et du backtesting est un mécanisme puissant pour orienter l’effort de modélisation vers une plus grande généralisation. En fait, elle est si efficace qu’il existe toute une classe d’algorithmes (d’apprentissage) qui intègre ce mécanisme même à leur cœur. Les plus remarquables sont les forêts aléatoires et les arbres boostés par gradient.
Briser la barrière dimensionnelle
Tout naturellement, plus on a de données, plus il y a d’informations à apprendre. Ainsi, toutes choses étant égales par ailleurs, plus de données devraient conduire à de meilleurs modèles, ou du moins à des modèles qui ne sont pas pires que leurs prédécesseurs. Après tout, si plus de données rendent le modèle moins bon, il est toujours possible d’ignorer les données en dernier recours. Pourtant, en raison des problèmes de surapprentissage, abandonner des données est resté la solution du “moindre mal” jusqu’à la fin des années 1990. C’était là le cœur du problème de la “barrière dimensionnelle”. Cette situation était à la fois déconcertante et profondément insatisfaisante. Les percées des années 1990 ont brisé les barrières dimensionnelles avec des idées étonnantes, à la fois théoriques et pratiques. Dans le processus, ces percées ont réussi à détourner - par la seule force de la distraction - l’ensemble du domaine d’étude pendant une décennie, retardant l’avènement de ses successeurs, principalement les méthodes d’apprentissage profond - discutées dans la section suivante.
Pour mieux comprendre ce qui n’allait pas avec avoir plus de données, considérons le scénario suivant : un fabricant fictif souhaite prédire le nombre de réparations non planifiées par an sur de grands équipements industriels. Après une réflexion approfondie sur le problème, l’équipe d’ingénierie a identifié trois facteurs indépendants qui semblent contribuer aux taux de défaillance. Cependant, la contribution respective de chaque facteur dans le taux de défaillance global n’est pas claire.
Ainsi, un modèle de régression linéaire simple avec 3 variables d’entrée est introduit. Le modèle peut être écrit comme Y = a1 * X1 + a2 * X2 + a3 * X3, où
- Y est la sortie du modèle linéaire (le taux de défaillance que les ingénieurs veulent prédire)
- X1, X2 et X3 sont les trois facteurs (types spécifiques de charges de travail exprimées en heures de fonctionnement) qui peuvent contribuer aux défaillances
- a1, a2 et a3 sont les trois paramètres du modèle qui doivent être identifiés.
Le nombre d’observations nécessaires pour obtenir des estimations “suffisamment bonnes” des trois paramètres dépend largement du niveau de bruit présent dans l’observation, et de ce qui est considéré comme “suffisamment bon”. Cependant, de manière intuitive, pour ajuster trois paramètres, il faudrait au minimum une vingtaine d’observations, même dans les situations les plus favorables. Comme les ingénieurs sont en mesure de collecter 100 observations, ils parviennent avec succès à régresser les 3 paramètres, et le modèle résultant semble “suffisamment bon” pour être d’intérêt pratique. Le modèle ne parvient pas à capturer de nombreux aspects des 100 observations, ce qui en fait une approximation très grossière, mais lorsque ce modèle est confronté à d’autres situations par le biais d’expériences de pensée, l’intuition et l’expérience disent aux ingénieurs que le modèle semble se comporter de manière raisonnable.
Forts de leur premier succès, les ingénieurs décident d’approfondir leurs recherches. Cette fois, ils exploitent l’ensemble des capteurs électroniques intégrés à la machinerie, et grâce aux enregistrements électroniques produits par ces capteurs, ils parviennent à augmenter l’ensemble des facteurs d’entrée à 10 000. Initialement, l’ensemble de données était composé de 100 observations, chaque observation étant caractérisée par 3 nombres. Maintenant, l’ensemble de données a été étendu ; il s’agit toujours des mêmes 100 observations, mais il y a 10 000 nombres par observation.
Cependant, lorsque les ingénieurs essaient d’appliquer la même approche à leur ensemble de données considérablement enrichi, le modèle linéaire ne fonctionne plus. Comme il y a 10 000 dimensions, le modèle linéaire est livré avec 10 000 paramètres ; et les 100 observations ne suffisent pas du tout à soutenir la régression de autant de paramètres. Le problème n’est pas qu’il est impossible de trouver des valeurs de paramètres qui s’ajustent, mais exactement le contraire : il est devenu trivial de trouver des ensembles infinis de paramètres qui s’ajustent parfaitement aux observations. Pourtant, aucun de ces modèles “ajustés” n’est d’une quelconque utilité pratique. Ces modèles “grands” s’ajustent parfaitement aux 100 observations, cependant, en dehors de ces observations, les modèles deviennent absurdes.
Les ingénieurs sont confrontés à la barrière dimensionnelle : apparemment, le nombre de paramètres doit rester petit par rapport aux observations, sinon l’effort de modélisation s’effondre. Ce problème est vexant car l’ensemble de données “plus grand”, avec 10 000 dimensions au lieu de 3, est évidemment plus informatif que le plus petit. Ainsi, un modèle statistique approprié devrait être capable de capturer ces informations supplémentaires au lieu de devenir dysfonctionnel lorsqu’il est confronté à celles-ci.
Au milieu des années 1990, une percée à double volet11, à la fois théorique et expérimentale, a bouleversé la communauté. La percée théorique était la théorie de Vapnik-Chervonenkis (VC)12. La théorie VC a prouvé que, en considérant des types spécifiques de modèles, l’erreur réelle pouvait être bornée supérieurement par ce qui équivalait grossièrement à la somme de l’erreur empirique plus le risque structurel, une propriété intrinsèque du modèle lui-même. Dans ce contexte, “erreur réelle” est l’erreur éprouvée sur les données que l’on ne possède pas, tandis que “erreur empirique” est l’erreur éprouvée sur les données que l’on possède. En minimisant la somme de l’erreur empirique et du risque structurel, l’erreur réelle pouvait être minimisée, car elle était “enfermée”. Cela représentait à la fois un résultat stupéfiant et probablement la plus grande avancée vers la généralisation depuis l’identification du problème de surapprentissage lui-même.
Sur le front expérimental, des modèles ultérieurement connus sous le nom de machines à vecteurs de support (SVM) ont été introduits presque comme une dérivation classique de ce que la théorie VC avait identifié sur l’apprentissage. Ces SVM sont devenus les premiers modèles largement réussis capables de faire un usage satisfaisant d’ensembles de données où le nombre de dimensions dépassait le nombre d’observations.
En enfermant l’erreur réelle, un résultat théorique vraiment surprenant, la théorie VC avait brisé la barrière dimensionnelle - quelque chose qui était resté vexant pendant près d’un siècle. Elle a également ouvert la voie à des modèles capables de tirer parti de données de haute dimension. Pourtant, assez rapidement, les SVM ont été remplacées par des modèles alternatifs, principalement des méthodes d’ensemble (forêts aléatoires13 et boosting), qui se sont révélées être des alternatives supérieures14 sur les fronts de la généralisation et des exigences de calcul. Comme les SVM qu’elles ont remplacées, les méthodes d’ensemble bénéficient également de garanties théoriques en ce qui concerne leur capacité à éviter le surapprentissage. Toutes ces méthodes partageaient la propriété d’être des méthodes non paramétriques. La barrière dimensionnelle avait été brisée grâce à l’introduction de modèles qui n’avaient pas besoin d’introduire un ou plusieurs paramètres pour chaque dimension ; évitant ainsi un chemin connu vers les problèmes de surapprentissage.
Revenons au problème des réparations non planifiées mentionné précédemment, contrairement aux modèles statistiques classiques - comme la régression linéaire, qui s’effondre face à la barrière dimensionnelle - les méthodes d’ensemble réussiraient à tirer parti de l’ensemble de données volumineux et de ses 10 000 dimensions même s’il n’y a que 100 observations. Qui plus est, les méthodes d’ensemble excelleraient plus ou moins d’emblée. Opérationnellement, il s’agissait d’un développement remarquable, car cela éliminait la nécessité de créer méticuleusement des modèles en choisissant l’ensemble d’entrée correctement précis.
L’impact sur la communauté plus large, tant au sein qu’en dehors du milieu universitaire, a été énorme. La plupart des efforts de recherche au début des années 2000 étaient consacrés à l’exploration de ces approches non paramétriques “théorie-soutenues”. Pourtant, les succès se sont rapidement évaporés au fil des années. En fait, une vingtaine d’années plus tard, les meilleurs modèles issus de ce qui est devenu connu sous le nom de perspective de “l’apprentissage statistique” restent les mêmes - bénéficiant simplement de mises en œuvre plus performantes15.
La double descente profonde
Jusqu’en 2010, la sagesse conventionnelle dictait que, pour éviter les problèmes de surapprentissage, le nombre de paramètres devait rester beaucoup plus petit que le nombre d’observations. En effet, chaque paramètre représentait implicitement un degré de liberté, et avoir autant de paramètres que d’observations était une recette pour garantir le surapprentissage16. Les méthodes d’ensemble ont contourné le problème en étant non paramétriques dès le départ. Pourtant, cette intuition critique s’est avérée fausse, et de manière spectaculaire.
Ce qui est devenu plus tard l’approche du deep learning a surpris presque toute la communauté grâce à des modèles hyperparamétriques. Ce sont des modèles qui ne surapprennent pas mais contiennent plusieurs fois plus de paramètres que d’observations.
La genèse du deep learning est complexe et peut être retracée jusqu’aux premières tentatives de modélisation des processus du cerveau, à savoir les réseaux neuronaux. Déballer cette genèse dépasse le cadre de la présente discussion, cependant, il convient de noter que la révolution du deep learning du début des années 2010 a commencé juste au moment où le domaine a abandonné la métaphore du réseau neuronal au profit de la sympathie mécanique. Les implémentations du deep learning ont remplacé les modèles précédents par des variantes beaucoup plus simples. Ces nouveaux modèles ont tiré parti de matériels informatiques alternatifs, notamment les GPU (unités de traitement graphique), qui se sont révélés, quelque peu accidentellement, bien adaptés aux opérations d’algèbre linéaire qui caractérisent les modèles de deep learning17.
Il a fallu près de cinq ans de plus pour que le deep learning soit largement reconnu comme une percée. Une partie importante de la réticence provenait du camp de l’apprentissage statistique - par coïncidence, la section de la communauté qui avait réussi à briser la barrière dimensionnelle deux décennies plus tôt. Bien que les explications varient pour cette réticence, la contradiction apparente entre la sagesse conventionnelle sur le surapprentissage et les revendications du deep learning a certainement contribué à un niveau appréciable de scepticisme initial concernant cette nouvelle classe de modèles.
La contradiction est restée largement non résolue jusqu’en 2019, lorsque la double descente profonde a été identifiée18, un phénomène qui caractérise le comportement de certaines classes de modèles. Pour de tels modèles, l’augmentation du nombre de paramètres dégrade d’abord l’erreur de test (par surapprentissage), jusqu’à ce que le nombre de paramètres devienne suffisamment grand pour inverser la tendance et améliorer à nouveau l’erreur de test. La “deuxième descente” (de l’erreur de test) n’était pas un comportement prédit par la perspective du compromis biais-variance.
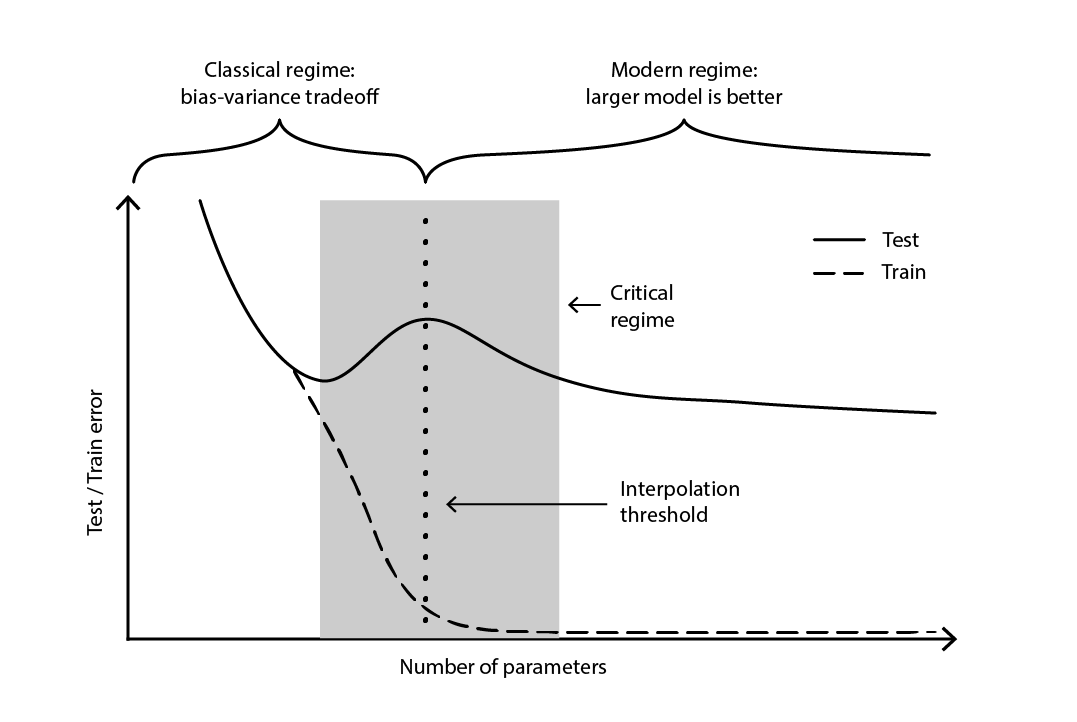
Figure 4. Une double descente profonde.
La figure 4 illustre les deux régimes successifs décrits ci-dessus. Le premier régime est le compromis classique biais-variance qui semble venir avec un nombre “optimal” de paramètres. Pourtant, ce minimum s’avère être un minimum local. Il existe un deuxième régime, observable si l’on continue d’augmenter le nombre de paramètres, qui présente une convergence asymptotique vers une erreur de test réellement optimale pour le modèle.
La double descente profonde a non seulement réconcilié les perspectives statistiques et d’apprentissage profond, mais a également démontré que la généralisation reste relativement peu comprise. Elle a prouvé que les théories largement répandues - courantes jusqu’à la fin des années 2010 - présentaient une perspective déformée de la généralisation. Cependant, la double descente profonde ne fournit pas encore de cadre - ou quelque chose d’équivalent - qui permettrait de prédire les capacités de généralisation (ou leur absence) des modèles en fonction de leur structure. À ce jour, l’approche reste résolument empirique.
Les épineux de la supply chain
Comme nous l’avons vu en détail, la généralisation est extrêmement difficile, et les chaînes d’approvisionnement ajoutent leur lot de particularités, intensifiant encore la situation. Premièrement, les données recherchées par les praticiens de la chaîne d’approvisionnement peuvent rester à jamais inaccessibles ; non pas partiellement invisibles, mais totalement inobservables. Deuxièmement, le simple fait de prédire peut altérer l’avenir et la validité de la prédiction, car les décisions sont basées sur ces prédictions mêmes. Ainsi, lorsqu’on aborde la généralisation dans un contexte de chaîne d’approvisionnement, une approche à deux volets doit être utilisée ; une jambe étant la solidité statistique du modèle et l’autre étant le raisonnement de haut niveau qui soutient le modèle.
De plus, les données disponibles ne sont pas toujours les données souhaitées. Prenons l’exemple d’un fabricant qui souhaite prévoir la demande afin de décider des quantités à produire. Il n’existe pas de données historiques de “demande”. À la place, les données de ventes historiques représentent le meilleur proxy disponible pour le fabricant afin de refléter la demande historique. Cependant, les ventes historiques sont faussées par les ruptures de stock passées. Les ventes nulles, causées par les ruptures de stock, ne doivent pas être confondues avec une demande nulle. Bien qu’un modèle puisse être élaboré pour rectifier cette historique des ventes en une sorte d’historique de la demande, l’erreur de généralisation de ce modèle est insaisissable par conception, car ni le passé ni le futur ne contiennent ces données. En bref, la “demande” est une construction nécessaire mais intangible.
Dans le jargon de l’apprentissage automatique, la modélisation de la demande est un problème d’apprentissage non supervisé où la sortie du modèle n’est jamais observée directement. Cet aspect non supervisé défait la plupart des algorithmes d’apprentissage, ainsi que la plupart des techniques de validation de modèle - du moins, dans leur version “naïve”. De plus, cela défait également l’idée même de compétition de prédiction, ici signifiant un processus simple en deux étapes où un ensemble de données original est divisé en un sous-ensemble public (d’entraînement) et un sous-ensemble privé (de validation). La validation elle-même devient un exercice de modélisation, par nécessité.
En termes simples, la prédiction créée par le fabricant façonnera, d’une manière ou d’une autre, l’avenir que le fabricant connaîtra. Une demande élevée projetée signifie que le fabricant augmentera sa production. Si l’entreprise est bien gérée, des économies d’échelle sont susceptibles d’être réalisées dans le processus de fabrication, ce qui réduit les coûts de production. À son tour, le fabricant est susceptible de profiter de ces nouvelles économies pour baisser les prix, ce qui lui confère un avantage concurrentiel par rapport à ses rivaux. Le marché, à la recherche de l’option la moins chère, peut rapidement adopter ce fabricant comme son option la plus compétitive, ce qui déclenche une augmentation de la demande bien au-delà de la projection initiale.
Ce phénomène est connu sous le nom de prophétie autoréalisatrice, une prédiction qui a tendance à devenir vraie en vertu de la croyance influente que les participants ont dans la prédiction elle-même. Une perspective non orthodoxe, mais pas entièrement déraisonnable, caractériserait les chaînes d’approvisionnement comme de gigantesques machines de Rube Goldberg autoréalisatrices. À un niveau méthodologique, cet enchevêtrement de l’observateur et de l’observation complique davantage la situation, car la généralisation est associée à la capture de l’intention stratégique qui sous-tend les développements de la chaîne d’approvisionnement.
À ce stade, le défi de la généralisation, tel qu’il se présente dans la chaîne d’approvisionnement, peut sembler insurmontable. Les feuilles de calcul, qui restent omniprésentes dans les chaînes d’approvisionnement, laissent certainement entendre que c’est la position par défaut, bien que implicite, de la plupart des entreprises. Une feuille de calcul est cependant avant tout un outil pour différer la résolution du problème à un jugement humain ad hoc, plutôt qu’à l’application d’une méthode systématique.
Bien que le recours au jugement humain soit invariablement une réponse incorrecte (en soi), ce n’est pas une réponse satisfaisante au problème non plus. La présence de ruptures de stock ne signifie pas que tout est permis en ce qui concerne la demande. Certes, si le fabricant a maintenu des taux de service moyens supérieurs à 90% au cours des trois dernières années, il serait très improbable que la demande (observée) puisse avoir été 10 fois supérieure aux ventes. Il est donc raisonnable de s’attendre à ce qu’une méthode systématique puisse être élaborée pour faire face à de telles distorsions. De même, la prophétie autoréalisatrice peut également être modélisée, notamment par le biais de la notion de politique telle que comprise par la théorie du contrôle.
Ainsi, lorsqu’on considère une chaîne d’approvisionnement réelle, la généralisation nécessite une approche à deux volets. Tout d’abord, le modèle doit être statistiquement solide, dans la mesure permise par les sciences de l’apprentissage “larges”. Cela englobe non seulement des perspectives théoriques telles que les statistiques classiques et l’apprentissage statistique, mais aussi des efforts empiriques tels que l’apprentissage automatique et les compétitions de prédiction. Revenir aux statistiques du XIXe siècle n’est pas une proposition raisonnable pour une pratique de la chaîne d’approvisionnement du XXIe siècle.
Deuxièmement, le modèle doit être soutenu par un raisonnement de haut niveau. En d’autres termes, pour chaque composant du modèle et chaque étape du processus de modélisation, il doit y avoir une justification qui a du sens d’un point de vue de la chaîne d’approvisionnement. Sans cet ingrédient, le chaos opérationnel19 est presque garanti, généralement déclenché par une évolution de la chaîne d’approvisionnement elle-même, de son écosystème opérationnel ou de son paysage applicatif sous-jacent. En effet, l’objectif principal du raisonnement de haut niveau n’est pas de faire fonctionner un modèle une fois, mais de le faire fonctionner de manière durable pendant plusieurs années dans un environnement en constante évolution. Ce raisonnement est l’ingrédient pas si secret qui aide à décider qu’il est temps de réviser le modèle lorsque sa conception, quelle qu’elle soit, n’est plus alignée avec la réalité et/ou les objectifs commerciaux.
De loin, cette proposition pourrait sembler vulnérable à la critique précédente adressée aux feuilles de calcul - celle de reporter le travail difficile à un “jugement humain” insaisissable. Bien que cette proposition reporte toujours l’évaluation du modèle au jugement humain, l’exécution du modèle est destinée à être entièrement automatisée. Ainsi, les opérations quotidiennes sont destinées à être entièrement automatisées, même si les efforts d’ingénierie en cours pour améliorer davantage les recettes numériques ne le sont pas.
Notes
-
Il existe une technique algorithmique importante appelée “mémorisation” qui remplace précisément un résultat qui pourrait être recalculé par son résultat précalculé, échangeant ainsi plus de mémoire contre moins de calcul. Cependant, cette technique n’est pas pertinente pour la présente discussion. ↩︎
-
Pourquoi la plupart des résultats de recherche publiés sont faux, John P. A. Ioannidis, août 2005 ↩︎
-
Du point de vue de la prévision des séries temporelles, la notion de généralisation est abordée par le concept de “précision”. La précision peut être considérée comme un cas particulier de “généralisation” lorsqu’on considère les séries temporelles. ↩︎
-
Makridakis, S.; Andersen, A.; Carbone, R.; Fildes, R.; Hibon, M.; Lewandowski, R.; Newton, J.; Parzen, E.; Winkler, R. (avril 1982). “The accuracy of extrapolation (time series) methods: Results of a forecasting competition”. Journal of Forecasting. 1 (2): 111–153. doi:10.1002/for.3980010202. ↩︎
-
Kaggle en chiffres, Carl McBride Ellis, consulté le 8 février 2023, ↩︎
-
L’extrait de 1935 “Peut-être sommes-nous démodés, mais pour nous, une analyse à six variables basée sur treize observations semble plutôt comme un surapprentissage”, tiré de “The Quarterly Review of Biology” (septembre 1935 Volume 10, numéro 3pp. 341 - 377), semble indiquer que le concept statistique de surapprentissage était déjà établi à cette époque. ↩︎
-
Grenander, Ulf. On empirical spectral analysis of stochastic processes. Ark. Mat., 1(6):503– 531, 08 1952. ↩︎
-
Whittle, P. Tests of Fit in Time Series, Vol. 39, No. 3/4 (Dec., 1952), pp. 309-318] (10 pages), Oxford University Press ↩︎
-
Everitt B.S., Skrondal A. (2010), Cambridge Dictionary of Statistics, Cambridge University Press. ↩︎
-
Les avantages asymptotiques de l’utilisation de valeurs k plus grandes pour le k-fold peuvent être déduits du théorème de la limite centrale. Cette observation suggère que, en augmentant k, nous pouvons obtenir une amélioration approximative de 1 / sqrt(k) de l’amélioration potentielle apportée par le k-fold en premier lieu. ↩︎
-
Réseaux de vecteurs de support, Corinna Cortes, Vladimir Vapnik, volume 20 de Machine Learning, pages 273–297 (1995) ↩︎
-
La théorie Vapnik-Chernovenkis (VC) n’était pas le seul candidat pour formaliser ce que signifie “apprendre”. Le cadre PAC (probably approximately correct) de Valiant en 1984 a ouvert la voie aux approches d’apprentissage formel. Cependant, le cadre PAC manquait de l’immense traction et des succès opérationnels dont a bénéficié la théorie VC autour du millénaire. ↩︎
-
Forêts aléatoires, Leo Breiman, volume 45 de Machine Learning, pages 5–32 (2001) ↩︎
-
L’une des conséquences malheureuses du fait que les machines à vecteurs de support (SVM) sont fortement inspirées par une théorie mathématique est que ces modèles ont peu de “sympathie mécanique” pour le matériel informatique moderne. L’inadéquation relative des SVM à traiter de grands ensembles de données - y compris des millions d’observations ou plus - par rapport aux alternatives a entraîné la chute de ces méthodes. ↩︎
-
XGBoost et LightGBM sont deux implémentations open-source des méthodes d’ensemble qui restent très populaires dans les cercles de l’apprentissage automatique. ↩︎
-
Pour des raisons de concision, il y a une certaine simplification ici. Il existe un domaine de recherche entier consacré à la “régularisation” des modèles statistiques. En présence de contraintes de régularisation, le nombre de paramètres, même en considérant un modèle classique comme une régression linéaire, peut dépasser en toute sécurité le nombre d’observations. En présence de régularisation, aucune valeur de paramètre ne représente vraiment un degré de liberté complet, mais plutôt une fraction de celui-ci. Ainsi, il serait plus approprié de se référer au nombre de degrés de liberté plutôt qu’au nombre de paramètres. Comme ces considérations tangentielles n’altèrent pas fondamentalement les points de vue présentés ici, la version simplifiée suffira. ↩︎
-
En fait, la causalité est inverse. Les pionniers du deep learning ont réussi à réingénierer leurs modèles d’origine - les réseaux neuronaux - en modèles plus simples qui reposaient presque exclusivement sur l’algèbre linéaire. Le but de cette réingénierie était précisément de rendre possible l’exécution de ces nouveaux modèles sur du matériel informatique qui échangeait la polyvalence contre la puissance brute, à savoir les GPU. ↩︎
-
Deep Double Descent: Où les modèles plus grands et plus de données nuisent, Preetum Nakkiran, Gal Kaplun, Yamini Bansal, Tristan Yang, Boaz Barak, Ilya Sutskever, décembre 2019 ↩︎
-
La grande majorité des initiatives de science des données dans la supply chain échouent. Mes observations occasionnelles indiquent que l’ignorance du data scientist de ce qui fait fonctionner la supply chain est la cause principale de la plupart de ces échecs. Bien qu’il soit incroyablement tentant - pour un data scientist nouvellement formé - de tirer parti du dernier package d’apprentissage automatique open-source le plus brillant, toutes les techniques de modélisation ne conviennent pas également pour soutenir le raisonnement de haut niveau. En fait, la plupart des techniques “grand public” sont tout simplement terribles lorsqu’il s’agit du processus de whiteboxing. ↩︎