Generalización (Pronóstico)
La generalización es la capacidad de un algoritmo para generar un modelo, aprovechando un conjunto de datos, que funcione bien en datos no vistos previamente. La generalización es de vital importancia para la cadena de suministro, ya que la mayoría de las decisiones reflejan una anticipación del futuro. En el contexto de pronóstico, los datos son invisibles porque el modelo predice eventos futuros, que son inobservables. Si bien se ha logrado un progreso sustancial, tanto teórico como práctico, en el frente de la generalización desde la década de 1990, la generalización “verdadera” sigue siendo esquiva. La resolución completa del problema de la generalización puede no ser muy diferente de la del problema de la inteligencia artificial general. Además, la cadena de suministro agrega su propia serie de desafíos espinosos a los desafíos generales convencionales.

Descripción general de una paradoja
Crear un modelo que funcione perfectamente en los datos que se tienen es sencillo: todo lo que se necesita es memorizar por completo el conjunto de datos y luego utilizar el propio conjunto de datos para responder cualquier consulta realizada sobre el conjunto de datos. Como las computadoras son buenas para registrar grandes conjuntos de datos, crear un modelo de este tipo es fácil. Sin embargo, también suele ser inútil1, ya que el verdadero valor de tener un modelo radica en su capacidad predictiva más allá de lo que ya se ha observado.
Se presenta un aparente paradójico ineludible: un buen modelo es aquel que funciona bien en datos que actualmente no están disponibles, pero, por definición, si los datos no están disponibles, el observador no puede realizar la evaluación. Por lo tanto, el término “generalización” se refiere a la capacidad esquiva de ciertos modelos para mantener su relevancia y calidad más allá de las observaciones disponibles en el momento en que se construye el modelo.
Si bien se puede descartar la memorización de las observaciones como una estrategia de modelado inadecuada, cualquier estrategia alternativa para crear un modelo puede estar sujeta al mismo problema. No importa cuán bien parezca que el modelo funciona en los datos actualmente disponibles, siempre es concebible que sea solo una cuestión de azar, o peor aún, un defecto de la estrategia de modelado. Lo que puede parecer en un principio una paradoja estadística marginal, de hecho, es un problema de gran alcance.
A modo de evidencia anecdótica, en 1979 la SEC (Comisión de Valores y Bolsa), la agencia estadounidense encargada de regular los mercados de capitales, introdujo su famosa Regla 156. Esta regla requiere que los gestores de fondos informen a los inversores que el rendimiento pasado no es indicativo de resultados futuros. El rendimiento pasado es implícitamente el “modelo” al que la SEC advierte que no se debe confiar por su poder de “generalización”; es decir, su capacidad para decir algo sobre el futuro.
Incluso la ciencia misma está luchando con lo que significa extrapolar “verdad” fuera de un conjunto limitado de observaciones. Los escándalos de “mala ciencia”, que se desarrollaron en la década de 2000 y 2010 en torno a la manipulación de p-valores, indican que campos enteros de investigación están dañados y no se pueden confiar2. Si bien hay casos de fraude flagrante en los que los datos experimentales han sido claramente manipulados, la mayor parte del tiempo, el meollo del problema radica en los modelos; es decir, en el proceso intelectual utilizado para generalizar lo que se ha observado.
Bajo su forma más amplia, el problema de la generalización es indistinguible del de la ciencia misma, por lo que es tan difícil como replicar la amplitud de la ingeniosidad y el potencial humano. Sin embargo, el enfoque estadístico más estrecho del problema de la generalización es mucho más accesible, y esta es la perspectiva que se adoptará en las próximas secciones.
Surgimiento de una nueva ciencia
La generalización surgió como un paradigma estadístico a principios del siglo XX, principalmente a través del prisma de la precisión de pronóstico3, que representa un caso especial estrechamente relacionado con los pronósticos de series de tiempo. A principios de la década de 1900, el surgimiento de una clase media propietaria de acciones en Estados Unidos generó un gran interés en métodos que ayudaran a las personas a obtener rendimientos financieros en sus activos comerciados. Tanto los adivinos como los pronosticadores económicos se dignaron a extrapolar eventos futuros para un público ansioso por pagar. Se hicieron fortunas y se perdieron, pero esos esfuerzos arrojaron muy poca luz sobre la “forma adecuada” de abordar el problema.
La generalización siguió siendo, en su mayor parte, un problema desconcertante durante la mayor parte del siglo XX. Ni siquiera estaba claro si pertenecía al ámbito de las ciencias naturales, gobernado por observaciones y experimentos, o al ámbito de la filosofía y las matemáticas, gobernado por la lógica y la autoconsistencia.
El espacio avanzó hasta un momento histórico en 1982, el año de la primera competencia de pronósticos pública, conocida coloquialmente como la competencia M4. El principio era sencillo: publicar un conjunto de datos de 1000 series de tiempo truncadas, permitir que los participantes envíen sus pronósticos y, finalmente, publicar el resto del conjunto de datos (las colas truncadas) junto con las precisiones alcanzadas por los participantes. A través de esta competencia, la generalización, aún vista a través del prisma de la precisión de pronóstico, había entrado en el ámbito de las ciencias naturales. A partir de entonces, las competencias de pronóstico se volvieron cada vez más frecuentes.
Unos pocos decenios más tarde, Kaggle, fundada en 2010, añadió una nueva dimensión a tales competencias al crear una plataforma dedicada a problemas generales de predicción (no solo de series de tiempo). Hasta febrero de 20235, la plataforma ha organizado 349 competencias con premios en efectivo. El principio sigue siendo el mismo que el de la competencia M original: se pone a disposición un conjunto de datos truncados, los participantes envían sus respuestas a las tareas de predicción dadas y, finalmente, se revelan las clasificaciones junto con la parte oculta del conjunto de datos. Las competencias siguen siendo el estándar de oro para la evaluación adecuada del error de generalización de los modelos.
Sobreajuste y subajuste
Sobreajuste, al igual que su antónimo subajuste, es un problema que surge con frecuencia al producir un modelo basado en un conjunto de datos dado, y socava el poder de generalización del modelo. Históricamente6, el sobreajuste surgió como el primer obstáculo bien comprendido para la generalización.
La visualización del sobreajuste se puede hacer utilizando un problema de modelado de series de tiempo simple. Para los fines de este ejemplo, supongamos que el objetivo es crear un modelo que refleje una serie de observaciones históricas. Una de las opciones más simples para modelar estas observaciones es un modelo lineal, como se ilustra a continuación (ver Figura 1).
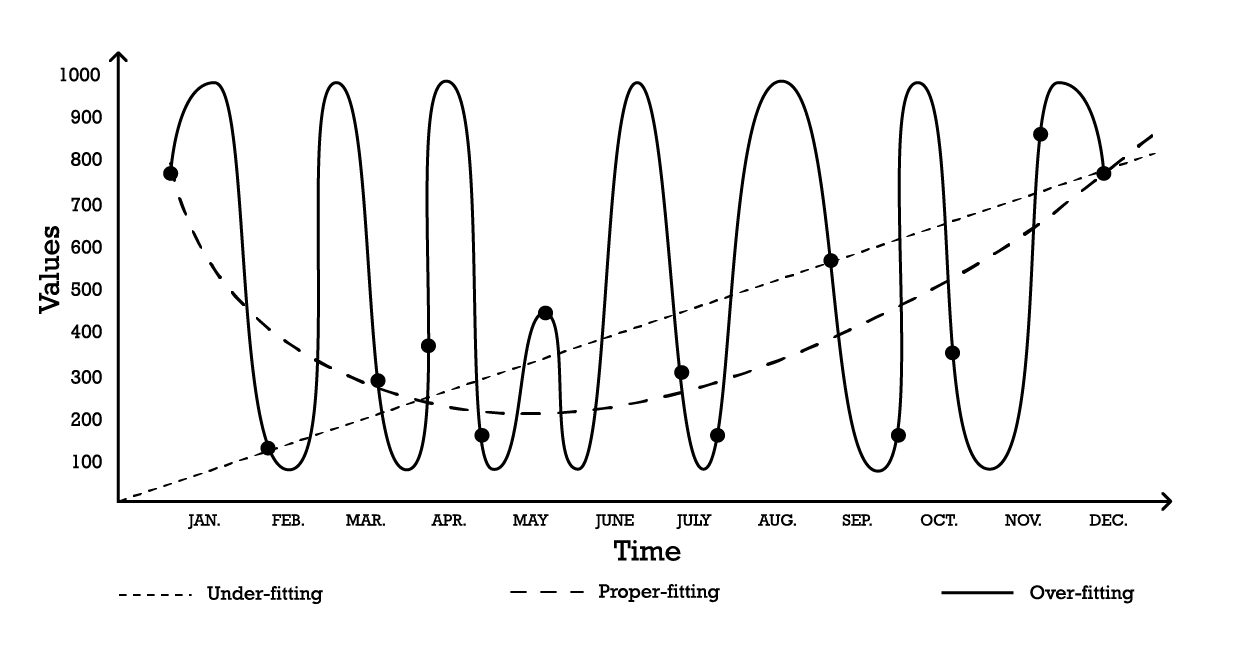
Figura 1: Un gráfico compuesto que muestra tres intentos diferentes de 'ajustar' una serie de observaciones.
Con dos parámetros, el modelo de “subajuste” es robusto, pero, como su nombre lo indica, subajusta los datos, ya que claramente no logra capturar la forma general de la distribución de las observaciones. Este enfoque lineal tiene un alto sesgo pero una baja varianza. En este contexto, sesgo debe entenderse como la limitación inherente de la estrategia de modelado para capturar los detalles de las observaciones, mientras que varianza debe entenderse como la sensibilidad a pequeñas fluctuaciones, posiblemente ruido, de las observaciones.
Se podría adoptar un modelo bastante complejo, como la curva de “sobreajuste” (Figura 1). Este modelo incluye muchos parámetros y se ajusta exactamente a las observaciones. Este enfoque tiene un bajo sesgo pero una varianza demostrablemente alta. Alternativamente, se podría adoptar un modelo de complejidad intermedia, como se ve en la curva de “ajuste adecuado” (Figura 1). Este modelo incluye tres parámetros, tiene un sesgo medio y una varianza media. De estas tres opciones, el modelo de ajuste adecuado es invariablemente el que mejor se desempeña en cuanto a la generalización.
Estas opciones de modelado representan la esencia del compromiso sesgo-varianza.7 8 El compromiso sesgo-varianza es un principio general que establece que el sesgo se puede reducir aumentando la varianza. El error de generalización se minimiza encontrando el equilibrio adecuado entre la cantidad de sesgo y varianza.
Históricamente, desde principios del siglo XX hasta principios de la década de 2010, se definía un modelo sobreajustado9 como aquel que contiene más parámetros de los que se pueden justificar con los datos. De hecho, a simple vista, agregar demasiados grados de libertad a un modelo parece ser la receta perfecta para problemas de sobreajuste. Sin embargo, la aparición del deep learning demostró que esta intuición y la definición de sobreajuste eran engañosas. Este punto se volverá a visitar en la sección sobre deep double-descent.
Validación cruzada y backtesting
La validación cruzada es una técnica de validación de modelos utilizada para evaluar qué tan bien un modelo se generalizará más allá de su conjunto de datos de soporte. Es un método de submuestreo que utiliza diferentes partes de los datos para probar y entrenar un modelo en diferentes iteraciones. La validación cruzada es el pan de cada día de las prácticas modernas de predicción, y casi todos los participantes ganadores de competencias de predicción hacen un uso extensivo de la validación cruzada.
Existen numerosas variantes de validación cruzada. La variante más popular es la validación k-fold, donde la muestra original se divide aleatoriamente en k submuestras. Cada submuestra se utiliza una vez como datos de validación, mientras que el resto, es decir, todas las demás submuestras, se utilizan como datos de entrenamiento.
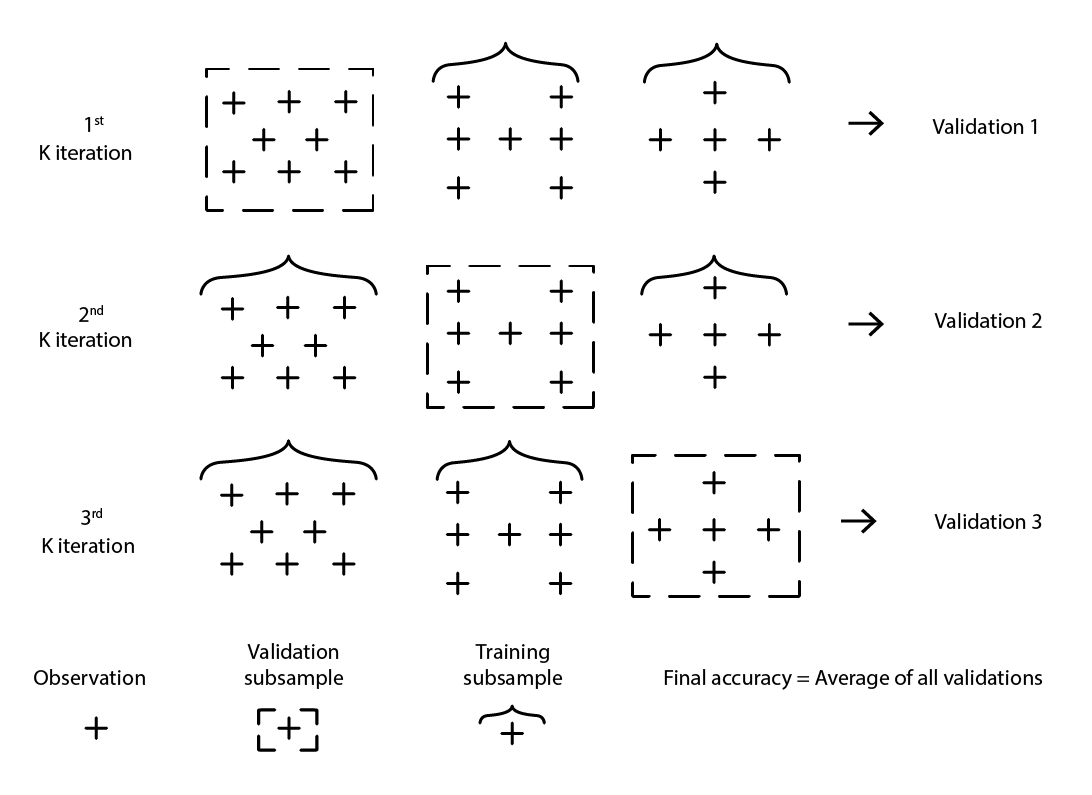
Figura 2: Una muestra de validación k-fold. Las observaciones anteriores son todas del mismo conjunto de datos. Por lo tanto, la técnica construye submuestras de datos para fines de validación y entrenamiento.
La elección del valor k, el número de submuestras, es un compromiso entre las ganancias estadísticas marginales y los requisitos en términos de recursos informáticos. De hecho, con la validación k-fold, los recursos informáticos crecen linealmente con el valor k, mientras que los beneficios, en términos de reducción del error, experimentan rendimientos decrecientes extremos10. En la práctica, seleccionar un valor de 10 o 20 para k suele ser “suficientemente bueno”, ya que las ganancias estadísticas asociadas con valores más altos no valen la pena la incomodidad adicional asociada con el mayor gasto de recursos informáticos.
La validación cruzada asume que el conjunto de datos se puede descomponer en una serie de observaciones independientes. Sin embargo, en la cadena de suministro, esto frecuentemente no es el caso, ya que el conjunto de datos generalmente refleja algún tipo de datos historizados donde existe una dependencia temporal. En presencia de tiempo, la submuestra de entrenamiento debe ser estrictamente “anterior” a la de validación. En otras palabras, el “futuro”, en relación con el punto de corte de remuestreo, no debe filtrarse en la submuestra de validación.
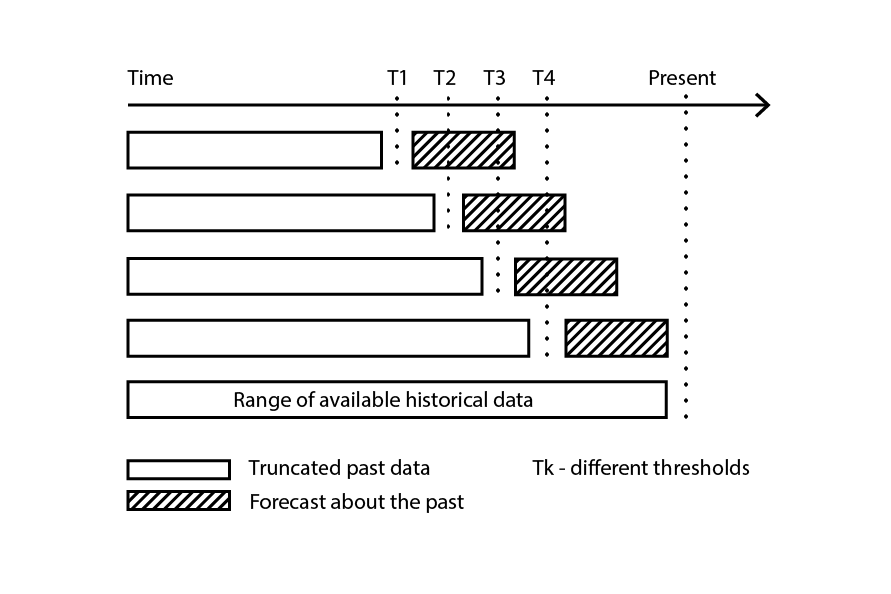
Figura 3: Un ejemplo de proceso de backtesting construye submuestras de datos para fines de validación y entrenamiento.
Backtesting representa la variante de validación cruzada que aborda directamente la dependencia temporal. En lugar de considerar submuestras aleatorias, los datos de entrenamiento y validación se obtienen respectivamente a través de un punto de corte: las observaciones anteriores al punto de corte pertenecen a los datos de entrenamiento, mientras que las observaciones posteriores al punto de corte pertenecen a los datos de validación. El proceso se repite seleccionando una serie de valores de corte distintos.
El método de remuestreo que se encuentra en el núcleo tanto de la validación cruzada como del backtesting es un mecanismo poderoso para dirigir el esfuerzo de modelado hacia un camino de mayor generalización. De hecho, es tan eficiente que existe una clase completa de algoritmos de (aprendizaje) automático que abrazan este mecanismo en su núcleo. Los más destacados son los bosques aleatorios y los árboles potenciados por gradientes.
Rompiendo la barrera dimensional
Bastante naturalmente, cuantos más datos se tengan, más información habrá para aprender. Por lo tanto, considerando todas las cosas iguales, más datos deberían llevar a mejores modelos, o al menos a modelos que no sean peores que sus predecesores. Después de todo, si más datos empeoran el modelo, siempre es posible ignorar los datos como último recurso. Sin embargo, debido a problemas de sobreajuste, deshacerse de los datos seguía siendo la solución “menos mala” hasta finales de la década de 1990. Este fue el meollo del problema de la “barrera dimensional”. Esta situación era tanto desconcertante como profundamente insatisfactoria. Los avances en la década de 1990 rompieron las barreras dimensionales con ideas sorprendentes, tanto teóricas como prácticas. En el proceso, esos avances lograron desviar, a través del puro poder de la distracción, todo el campo de estudio durante una década, retrasando el advenimiento de sus sucesores, principalmente los métodos de aprendizaje profundo, que se discuten en la siguiente sección.
Para comprender mejor lo que solía estar mal con “tener más datos”, consideremos el siguiente escenario: un fabricante ficticio quiere predecir el número de reparaciones no programadas por año en grandes equipos industriales. Después de una cuidadosa consideración del problema, el equipo de ingeniería ha identificado tres factores independientes que parecen contribuir a las tasas de falla. Sin embargo, la contribución respectiva de cada factor en la tasa de falla general no está clara.
Por lo tanto, se introduce un modelo de regresión lineal simple con 3 variables de entrada. El modelo se puede escribir como Y = a1 * X1 + a2 * X2 + a3 * X3, donde
- Y es la salida del modelo lineal (la tasa de falla que los ingenieros quieren predecir)
- X1, X2 y X3 son los tres factores (tipos específicos de cargas de trabajo expresadas en horas de operación) que pueden contribuir a las fallas
- a1, a2 y a3 son los tres parámetros del modelo que se deben identificar.
La cantidad de observaciones necesarias para obtener estimaciones “suficientemente buenas” para los tres parámetros depende en gran medida del nivel de ruido presente en la observación y de lo que se considera “suficientemente bueno”. Sin embargo, intuitivamente, para ajustar tres parámetros, se requerirían al menos dos docenas de observaciones, incluso en las situaciones más favorables. A medida que los ingenieros pueden recopilar 100 observaciones, logran regresar exitosamente 3 parámetros, y el modelo resultante parece “suficientemente bueno” para ser de interés práctico. El modelo no logra capturar muchos aspectos de las 100 observaciones, lo que lo convierte en una aproximación muy aproximada, pero cuando se desafía este modelo con otras situaciones a través de experimentos mentales, la intuición y la experiencia les dicen a los ingenieros que el modelo parece comportarse razonablemente.
Basándose en su primer éxito, los ingenieros deciden investigar más a fondo. Esta vez, aprovechan toda la gama de sensores electrónicos incorporados en la maquinaria y, a través de los registros electrónicos producidos por esos sensores, logran aumentar el conjunto de factores de entrada a 10,000. Inicialmente, el conjunto de datos estaba compuesto por 100 observaciones, cada una caracterizada por 3 números. Ahora, el conjunto de datos se ha expandido; todavía son las mismas 100 observaciones, pero hay 10,000 números por observación.
Sin embargo, cuando los ingenieros intentan aplicar el mismo enfoque a su conjunto de datos enriquecido, el modelo lineal ya no funciona. Como hay 10,000 dimensiones, el modelo lineal viene con 10,000 parámetros; y las 100 observaciones están lejos de ser suficientes para soportar la regresión de tantos parámetros. El problema no es que sea imposible encontrar valores de parámetros que se ajusten, sino todo lo contrario: se ha vuelto trivial encontrar conjuntos infinitos de parámetros que se ajusten perfectamente a las observaciones. Sin embargo, ninguno de estos modelos “ajustados” tiene ningún uso práctico. Estos modelos “grandes” se ajustan perfectamente a las 100 observaciones, pero fuera de esas observaciones, los modelos se vuelven absurdos.
Los ingenieros se enfrentan a la barrera dimensional: aparentemente, el número de parámetros debe seguir siendo pequeño en comparación con las observaciones, de lo contrario, el esfuerzo de modelado se desmorona. Este problema es desalentador ya que el conjunto de datos “más grande”, con 10,000 dimensiones en lugar de 3, es obviamente más informativo que el más pequeño. Por lo tanto, un modelo estadístico adecuado debería ser capaz de capturar esta información adicional en lugar de volverse disfuncional cuando se enfrenta a ella.
A mediados de la década de 1990, se produjo un avance doble11, tanto teórico como experimental, que sorprendió a la comunidad. El avance teórico fue la teoría de Vapnik-Chervonenkis (VC)12. La teoría de VC demostró que, considerando tipos específicos de modelos, el error real podría estar acotado superiormente por lo que se podría considerar una suma del error empírico más el riesgo estructural, una propiedad intrínseca del propio modelo. En este contexto, “error real” es el error experimentado en los datos que uno no tiene, mientras que “error empírico” es el error experimentado en los datos que uno tiene. Al minimizar la suma del error empírico y el riesgo estructural, se podría minimizar el error real, ya que estaba “encerrado”. Esto representó tanto un resultado sorprendente como el paso más importante hacia la generalización desde la identificación del problema de sobreajuste.
En el frente experimental, se introdujeron modelos conocidos posteriormente como Máquinas de Vectores de Soporte (SVM, por sus siglas en inglés) casi como una derivación de libro de texto de lo que la teoría de VC había identificado sobre el aprendizaje. Estas SVM se convirtieron en los primeros modelos ampliamente exitosos capaces de hacer un uso satisfactorio de conjuntos de datos donde el número de dimensiones superaba el número de observaciones.
Al encerrar el error real, un resultado teórico realmente sorprendente, la teoría de VC había roto la barrera dimensional, algo que había sido desalentador durante casi un siglo. También abrió el camino para modelos capaces de aprovechar datos de alta dimensionalidad. Sin embargo, bastante pronto, las SVM fueron desplazadas por modelos alternativos, principalmente métodos de conjunto (bosques aleatorios13 y aumento de gradiente), que demostraron ser alternativas superiores en los años 2000, prevaleciendo tanto en la generalización como en los requisitos de computación. Al igual que las SVM que reemplazaron, los métodos de conjunto también se benefician de garantías teóricas con respecto a su capacidad para evitar el sobreajuste. Todos estos métodos comparten la propiedad de ser métodos no paramétricos. La barrera dimensional se había roto mediante la introducción de modelos que no necesitaban introducir uno o más parámetros por cada dimensión, evitando así un camino conocido hacia los problemas de sobreajuste.
Volviendo al problema de las reparaciones no programadas mencionado anteriormente, a diferencia de los modelos estadísticos clásicos, como la regresión lineal, que se desmoronan frente a la barrera dimensional, los métodos de conjunto lograrían aprovechar el gran conjunto de datos y sus 10,000 dimensiones incluso si solo hay 100 observaciones. Además, los métodos de conjunto destacarían más o menos tal cual están. Operativamente, esto fue un desarrollo bastante notable, ya que eliminó la necesidad de crear meticulosamente modelos eligiendo el conjunto de dimensiones de entrada precisamente correcto.
El impacto en la comunidad en general, tanto dentro como fuera de la academia, fue enorme. La mayoría de los esfuerzos de investigación a principios de los años 2000 se dedicaron a explorar estos enfoques no paramétricos “respaldados por la teoría”. Sin embargo, los éxitos se evaporaron rápidamente a medida que pasaron los años. De hecho, unos veinte años después, los mejores modelos de lo que se conoció como la perspectiva de “aprendizaje estadístico” siguen siendo los mismos, simplemente beneficiándose de implementaciones más eficientes14.
La doble caída profunda
Hasta 2010, la sabiduría convencional dictaba que, para evitar problemas de sobreajuste, el número de parámetros debía ser mucho menor que el número de observaciones. De hecho, como cada parámetro representaba implícitamente un grado de libertad, tener tantos parámetros como observaciones era una receta para garantizar el sobreajuste15. Los métodos de conjunto resolvieron el problema al ser no paramétricos en primer lugar. Sin embargo, resultó que esta idea crítica estaba equivocada, y de manera espectacular.
Lo que más tarde se conoció como el enfoque de aprendizaje profundo sorprendió a casi toda la comunidad a través de modelos hiperparamétricos. Estos son modelos que no sufren de sobreajuste pero contienen muchas veces más parámetros que observaciones.
El origen del aprendizaje profundo es complejo y se remonta a los primeros intentos de modelar los procesos del cerebro, es decir, las redes neuronales. Desentrañar este origen está más allá del alcance de la presente discusión, sin embargo, vale la pena señalar que la revolución del aprendizaje profundo a principios de los años 2010 comenzó justo cuando el campo abandonó la metáfora de la red neuronal a favor de la simpatía mecánica. Las implementaciones de aprendizaje profundo reemplazaron los modelos anteriores con variantes mucho más simples. Estos modelos más nuevos aprovecharon hardware de computación alternativo, especialmente las GPUs (unidades de procesamiento gráfico), que resultaron ser, de manera algo accidental, adecuadas para las operaciones de álgebra lineal que caracterizan a los modelos de aprendizaje profundo16.
Pasaron casi cinco años más para que el aprendizaje profundo fuera ampliamente reconocido como un avance. Gran parte de la reticencia provino del campo del “aprendizaje estadístico”, coincidentemente, la sección de la comunidad que había logrado romper la barrera dimensional dos décadas antes. Si bien las explicaciones varían para esta reticencia, la aparente contradicción entre la sabiduría convencional sobre el sobreajuste y las afirmaciones del aprendizaje profundo ciertamente contribuyeron a un nivel apreciable de escepticismo inicial con respecto a esta nueva clase de modelos.
La contradicción se mantuvo en gran medida sin resolver hasta 2019, cuando se identificó la doble caída profunda17, un fenómeno que caracteriza el comportamiento de ciertas clases de modelos. Para estos modelos, aumentar el número de parámetros primero degrada el error de prueba (a través del sobreajuste), hasta que el número de parámetros se vuelve lo suficientemente grande como para revertir la tendencia y mejorar nuevamente el error de prueba. La “segunda caída” (del error de prueba) no era un comportamiento predicho por la perspectiva de compensación de sesgo.
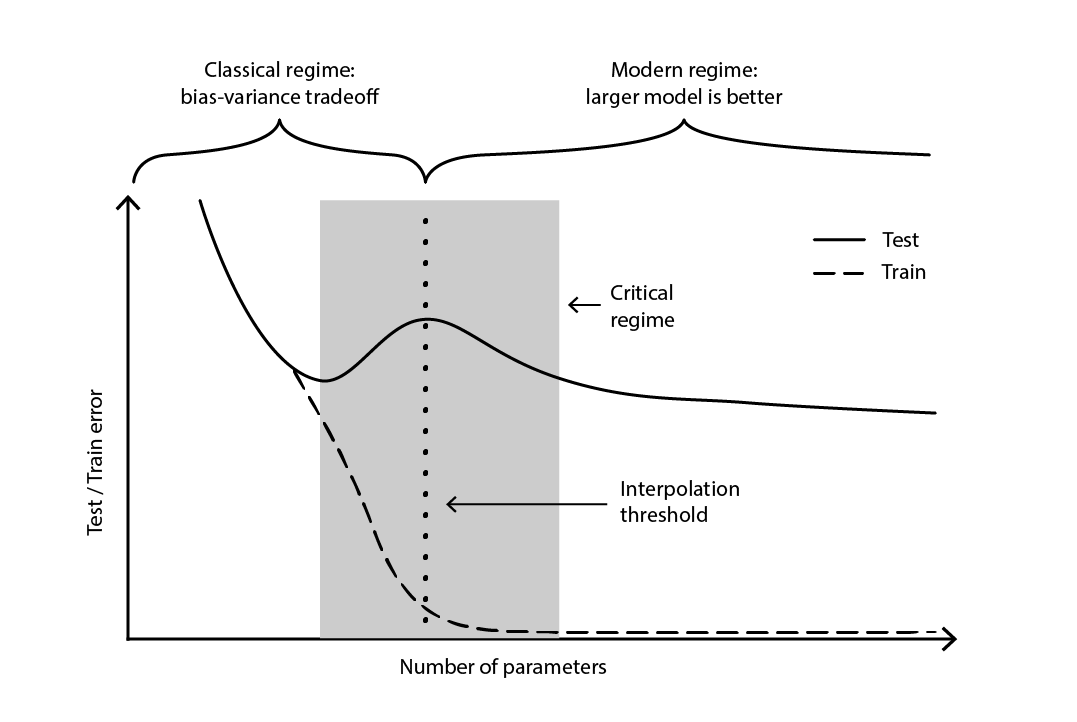
Figura 4. Una doble caída profunda.
La Figura 4 ilustra los dos regímenes sucesivos descritos anteriormente. El primer régimen es el clásico compromiso sesgo-varianza que aparentemente viene con un número “óptimo” de parámetros. Sin embargo, este mínimo resulta ser un mínimo local. Hay un segundo régimen, observable si se sigue aumentando el número de parámetros, que muestra una convergencia asintótica hacia un error de prueba óptimo real para el modelo.
La doble caída profunda no solo reconcilió las perspectivas del aprendizaje estadístico y el aprendizaje profundo, sino que también demostró que la generalización sigue siendo relativamente poco comprendida. Demostró que las teorías ampliamente aceptadas, comunes hasta finales de la década de 2010, presentaban una perspectiva distorsionada sobre la generalización. Sin embargo, la doble caída profunda aún no proporciona un marco, o algo equivalente, que prediga los poderes de generalización (o la falta de ellos) de los modelos basados en su estructura. Hasta la fecha, el enfoque sigue siendo resueltamente empírico.
Las espinas de la cadena de suministro
Como se ha cubierto en profundidad, la generalización es extremadamente desafiante, y las cadenas de suministro logran agregar sus propias peculiaridades, intensificando aún más la situación. En primer lugar, los datos que los profesionales de la cadena de suministro buscan pueden permanecer inaccesibles para siempre; no parcialmente invisibles, sino completamente inobservables. En segundo lugar, el simple acto de predecir puede alterar el futuro y la validez de la predicción, ya que las decisiones se basan en esas mismas predicciones. Por lo tanto, al abordar la generalización en un contexto de cadena de suministro, se debe utilizar un enfoque de dos patas; una pata es la solidez estadística del modelo y la otra es el razonamiento de alto nivel que respalda el modelo.
Además, los datos disponibles no siempre son los datos deseados. Considere un fabricante que desea pronosticar la demanda para decidir las cantidades a producir. No existe tal cosa como datos históricos de “demanda”. En cambio, los datos de ventas históricas representan el mejor proxy disponible para el fabricante para reflejar la demanda histórica. Sin embargo, las ventas históricas están distorsionadas por desabastecimientos pasados. Las ventas nulas, causadas por desabastecimientos, no deben confundirse con una demanda nula. Si bien se puede crear un modelo para rectificar este historial de ventas en algún tipo de historial de demanda, el error de generalización de este modelo es esquivo por diseño, ya que ni el pasado ni el futuro contienen estos datos. En resumen, “demanda” es una construcción necesaria pero intangible.
En el argot del aprendizaje automático, modelar la demanda es un problema de aprendizaje no supervisado en el que la salida del modelo nunca se observa directamente. Este aspecto no supervisado derrota a la mayoría de los algoritmos de aprendizaje y también a la mayoría de las técnicas de validación de modelos, al menos en su versión “ingenua”. Además, también derrota la idea misma de una competencia de predicción, aquí entendida como un proceso simple de dos etapas en el que un conjunto de datos original se divide en un subconjunto público (entrenamiento) y un subconjunto privado (validación). La validación en sí misma se convierte en un ejercicio de modelado, por necesidad.
En pocas palabras, la predicción creada por el fabricante dará forma, de una manera u otra, al futuro que el fabricante experimenta. Una alta demanda proyectada significa que el fabricante aumentará la producción. Si el negocio está bien administrado, es probable que se logren economías de escala en el proceso de fabricación, lo que reduce los costos de producción. A su vez, es probable que el fabricante aproveche estas nuevas economías para reducir los precios, obteniendo así una ventaja competitiva sobre sus competidores. El mercado, buscando la opción más económica, puede adoptar rápidamente a este fabricante como su opción más competitiva, lo que desencadena un aumento de la demanda mucho más allá de la proyección inicial.
Este fenómeno se conoce como una profecía autocumplida, una predicción que tiende a hacerse realidad por virtud de la creencia influyente que los participantes tienen en la propia predicción. Una perspectiva poco ortodoxa, pero no del todo irrazonable, caracterizaría las cadenas de suministro como gigantescos artefactos de Rube Goldberg autocumplidos. A nivel metodológico, este enredo de observador y observación complica aún más la situación, ya que la generalización se asocia con la captura de la intención estratégica que subyace en los desarrollos de la cadena de suministro.
En este punto, el desafío de la generalización, tal como se presenta en la cadena de suministro, puede parecer insuperable. Las hojas de cálculo, que siguen siendo omnipresentes en las cadenas de suministro, ciertamente insinúan que esta es la posición predeterminada, aunque implícita, de la mayoría de las empresas. Sin embargo, una hoja de cálculo es, ante todo, una herramienta para posponer la resolución del problema a algún juicio humano ad hoc, en lugar de la aplicación de algún método sistemático.
Aunque recurrir al juicio humano es invariablemente una respuesta incorrecta (en sí misma), tampoco es una respuesta satisfactoria al problema. La presencia de desabastecimientos no significa que todo vale en lo que respecta a la demanda. Ciertamente, si el fabricante ha mantenido niveles de servicio promedio por encima del 90% durante los últimos tres años, sería muy improbable que la demanda (observada) pudiera haber sido 10 veces mayor que las ventas. Por lo tanto, es razonable esperar que se pueda diseñar un método sistemático para hacer frente a tales distorsiones. De manera similar, la profecía autocumplida también se puede modelar, especialmente a través de la noción de política tal como se entiende en la teoría del control.
Por lo tanto, al considerar una cadena de suministro del mundo real, la generalización requiere un enfoque de dos patas. En primer lugar, el modelo debe ser estadísticamente sólido, en la medida en que lo permitan las amplias ciencias del “aprendizaje”. Esto abarca no solo perspectivas teóricas como la estadística clásica y el aprendizaje estadístico, sino también esfuerzos empíricos como el aprendizaje automático y las competencias de predicción. Revertir a la estadística del siglo XIX no es una propuesta razonable para la práctica de la cadena de suministro del siglo XXI.
En segundo lugar, el modelo debe estar respaldado por un razonamiento de alto nivel. En otras palabras, para cada componente del modelo y cada paso del proceso de modelado, debe haber una justificación que tenga sentido desde una perspectiva de cadena de suministro. Sin este ingrediente, el caos operativo18 está casi garantizado, generalmente desencadenado por alguna evolución de la propia cadena de suministro, su ecosistema operativo o su paisaje aplicativo subyacente. De hecho, el punto principal del razonamiento de alto nivel no es hacer que un modelo funcione una vez, sino hacer que funcione de manera sostenible a lo largo de varios años en un entorno en constante cambio. Este razonamiento es el ingrediente no tan secreto que ayuda a decidir cuándo es el momento de revisar el modelo cuando su diseño, sea cual sea, ya no se alinea con la realidad y/o los objetivos comerciales.
Desde lejos, esta propuesta podría parecer vulnerable a la crítica anterior dirigida a las hojas de cálculo: la que se opone a delegar el trabajo duro en algún “juicio humano” elusivo. Aunque esta propuesta todavía pospone la evaluación del modelo al juicio humano, la ejecución del modelo está destinada a ser completamente automatizada. Por lo tanto, las operaciones diarias están destinadas a ser completamente automatizadas, incluso si los esfuerzos de ingeniería en curso para mejorar aún más las recetas numéricas no lo son.
Notas
-
Existe una importante técnica algorítmica llamada “memoización” que reemplaza precisamente un resultado que podría ser recomputado por su resultado precomputado, intercambiando así más memoria por menos cálculo. Sin embargo, esta técnica no es relevante para la presente discusión. ↩︎
-
Por qué la mayoría de los hallazgos de investigación publicados son falsos, John P. A. Ioannidis, agosto de 2005 ↩︎
-
Desde la perspectiva del pronóstico de series temporales, la noción de generalización se aborda a través del concepto de “exactitud”. La exactitud se puede ver como un caso especial de “generalización” al considerar series temporales. ↩︎
-
Makridakis, S.; Andersen, A.; Carbone, R.; Fildes, R.; Hibon, M.; Lewandowski, R.; Newton, J.; Parzen, E.; Winkler, R. (abril de 1982). “La precisión de los métodos de extrapolación (series temporales): resultados de una competencia de pronóstico”. Journal of Forecasting. 1 (2): 111–153. doi:10.1002/for.3980010202. ↩︎
-
Kaggle en números, Carl McBride Ellis, consultado el 8 de febrero de 2023, ↩︎
-
El fragmento de 1935 “Quizás seamos anticuados, pero para nosotros un análisis de seis variables basado en trece observaciones parece más bien un caso de sobreajuste”, de “The Quarterly Review of Biology” (sep, 1935 Volumen 10, Número 3pp. 341 - 377), parece indicar que el concepto estadístico de sobreajuste ya estaba establecido en ese momento. ↩︎
-
Grenander, Ulf. Sobre el análisis espectral empírico de procesos estocásticos. Ark. Mat., 1(6):503– 531, 08 1952. ↩︎
-
Whittle, P. Pruebas de ajuste en series temporales, Vol. 39, No. 3/4 (dic., 1952), pp. 309-318] (10 páginas), Oxford University Press ↩︎
-
Everitt B.S., Skrondal A. (2010), Diccionario de Estadística de Cambridge, Cambridge University Press. ↩︎
-
Los beneficios asintóticos de usar valores k mayores para el k-fold se pueden inferir del teorema del límite central. Esta idea sugiere que, al aumentar k, podemos acercarnos aproximadamente a 1 / sqrt(k) de agotar todo el potencial de mejora que aporta el k-fold en primer lugar. ↩︎
-
Redes de vectores de soporte, Corinna Cortes, Vladimir Vapnik, Machine Learning volumen 20, páginas 273–297 (1995) ↩︎
-
La teoría de Vapnik-Chernovenkis (VC) no fue la única candidata para formalizar lo que significa “aprendizaje”. El marco PAC (probablemente aproximadamente correcto) de Valiant en 1984 abrió el camino para enfoques formales de aprendizaje. Sin embargo, el marco PAC carecía de la inmensa tracción y los éxitos operativos que la teoría VC disfrutó alrededor del milenio. ↩︎
-
Bosques aleatorios, Leo Breiman, Machine Learning volumen 45, páginas 5–32 (2001) ↩︎
-
XGBoost y LightGBM son dos implementaciones de código abierto de los métodos de conjunto que siguen siendo ampliamente populares en los círculos de aprendizaje automático. ↩︎
-
Por una cuestión de concisión, aquí se está simplificando un poco. Existe todo un campo de investigación dedicado a la “regularización” de modelos estadísticos. En presencia de restricciones de regularización, el número de parámetros, incluso considerando un modelo clásico como una regresión lineal, puede superar de manera segura el número de observaciones. En presencia de regularización, ningún valor de parámetro representa realmente un grado completo de libertad, sino más bien una fracción de uno. Por lo tanto, sería más apropiado referirse al número de grados de libertad en lugar de referirse al número de parámetros. Dado que estas consideraciones tangenciales no alteran fundamentalmente las opiniones presentadas aquí, la versión simplificada será suficiente. ↩︎
-
De hecho, la causalidad es la inversa. Los pioneros del aprendizaje profundo lograron rediseñar sus modelos originales, las redes neuronales, en modelos más simples que se basaban casi exclusivamente en álgebra lineal. El objetivo de esta reingeniería era precisamente hacer posible ejecutar estos modelos más nuevos en hardware informático que intercambiaba versatilidad por potencia bruta, es decir, las GPUs. ↩︎
-
Doble descenso profundo: dónde los modelos más grandes y más datos perjudican, Preetum Nakkiran, Gal Kaplun, Yamini Bansal, Tristan Yang, Boaz Barak, Ilya Sutskever, diciembre de 2019 ↩︎
-
La gran mayoría de las iniciativas de ciencia de datos en la cadena de suministro fracasan. Mis observaciones informales indican que la ignorancia del científico de datos sobre lo que hace que la cadena de suministro funcione es la causa principal de la mayoría de estos fracasos. Aunque es increíblemente tentador, para un científico de datos recién capacitado, aprovechar el paquete de aprendizaje automático de código abierto más reciente y brillante, no todas las técnicas de modelado son igualmente adecuadas para respaldar el razonamiento de alto nivel. De hecho, la mayoría de las técnicas “convencionales” son realmente terribles cuando se trata del proceso de “whiteboxing”. ↩︎