Generalisierung (Prognostizieren)
Generalisierung ist die Fähigkeit eines Algorithmus, ein Modell zu generieren - basierend auf einem Datensatz -, das auf zuvor ungesehenen Daten gut funktioniert. Generalisierung ist von entscheidender Bedeutung für die Supply Chain, da die meisten Entscheidungen eine Vorwegnahme der Zukunft darstellen. Im Prognosekontext sind die Daten unsichtbar, da das Modell zukünftige Ereignisse vorhersagt, die nicht beobachtbar sind. Obwohl seit den 1990er Jahren erhebliche Fortschritte sowohl theoretischer als auch praktischer Natur auf dem Gebiet der Generalisierung erzielt wurden, bleibt die wahre Generalisierung schwer fassbar. Die vollständige Lösung des Generalisierungsproblems unterscheidet sich möglicherweise nicht wesentlich von der Lösung des Problems der künstlichen allgemeinen Intelligenz. Darüber hinaus bringt die Supply Chain ihre eigenen Probleme mit sich, die über die allgemeinen Herausforderungen der Generalisierung hinausgehen.

Überblick über ein Paradoxon
Das Erstellen eines Modells, das perfekt auf den vorhandenen Daten funktioniert, ist einfach: Es genügt, den Datensatz vollständig auswendig zu lernen und dann den Datensatz selbst zu verwenden, um jede Abfrage zu beantworten, die über den Datensatz gestellt wird. Da Computer gut darin sind, große Datensätze aufzuzeichnen, ist es einfach, ein solches Modell zu entwickeln. Es ist jedoch in der Regel sinnlos1, da der gesamte Nutzen eines Modells in seiner Vorhersagekraft liegt, die über das bereits Beobachtete hinausgeht.
Es ergibt sich ein scheinbar unausweichliches Paradoxon: Ein gutes Modell ist eines, das auf Daten gut funktioniert, die derzeit nicht verfügbar sind, aber per Definition kann der Beobachter die Bewertung nicht durchführen, wenn die Daten nicht verfügbar sind. Der Begriff “Generalisierung” bezieht sich daher auf die schwer fassbare Fähigkeit bestimmter Modelle, ihre Relevanz und Qualität über die zum Zeitpunkt der Modellerstellung verfügbaren Beobachtungen hinaus beizubehalten.
Während das Auswendiglernen der Beobachtungen als unzureichende Modellierungsstrategie abgetan werden kann, ist jede alternative Strategie zur Erstellung eines Modells potenziell demselben Problem ausgesetzt. Unabhängig davon, wie gut das Modell auf den derzeit verfügbaren Daten zu funktionieren scheint, ist es immer möglich, dass es nur eine Frage des Zufalls oder noch schlimmer, ein Fehler der Modellierungsstrategie ist. Was zunächst als Randerscheinung eines statistischen Paradoxons erscheinen mag, ist in Wirklichkeit ein weitreichendes Problem.
Als beispielhafter Beweis führte die SEC (Securities and Exchange Commission), die US-Behörde zur Regulierung der Kapitalmärkte, im Jahr 1979 ihre berühmte Rule 156 ein. Diese Regel verpflichtet Fondsmanager, Anleger darauf hinzuweisen, dass die vergangene Performance keine Rückschlüsse auf zukünftige Ergebnisse zulässt. Die vergangene Performance ist implizit das “Modell”, dem die SEC rät, nicht auf seine “Generalisierung” zu vertrauen, d.h. seine Fähigkeit, etwas über die Zukunft auszusagen.
Selbst die Wissenschaft selbst hat Schwierigkeiten, “Wahrheit” außerhalb einer engen Beobachtungsreihe zu extrapolieren. Die Skandale um “schlechte Wissenschaft”, die sich in den 2000er und 2010er Jahren um p-Hacking entwickelten, deuten darauf hin, dass ganze Forschungsfelder fehlerhaft sind und nicht vertrauenswürdig sind2. Während es Fälle von offensichtlichem Betrug gibt, bei denen die experimentellen Daten offensichtlich manipuliert wurden, liegt das Kernproblem meistens in den Modellen; das heißt, im intellektuellen Prozess, der verwendet wird, um das Beobachtete zu generalisieren.
Unter seinem weitreichendsten Gesichtspunkt ist das Generalisierungsproblem von der Wissenschaft selbst nicht zu unterscheiden, daher ist es so schwierig wie die Nachbildung der Vielfalt menschlicher Genialität und Potenziale. Dennoch ist das engere statistische Verständnis des Generalisierungsproblems viel zugänglicher, und dies ist die Perspektive, die in den kommenden Abschnitten eingenommen wird.
Entstehung einer neuen Wissenschaft
Generalisierung entwickelte sich als statistisches Paradigma zu Beginn des 20. Jahrhunderts, hauptsächlich durch die Linse der Prognosegenauigkeit3, die ein eng mit Zeitreihenprognosen verbundener Sonderfall darstellt. In den frühen 1900er Jahren erzeugte das Aufkommen einer mittelständischen Klasse von Aktienbesitzern in den USA ein enormes Interesse an Methoden, die den Menschen helfen würden, finanzielle Erträge aus ihren gehandelten Vermögenswerten zu erzielen. Wahrsager und Wirtschaftsprognostiker versuchten gleichermaßen, zukünftige Ereignisse für ein zahlungsbereites Publikum zu extrapolieren. Fortunes wurden gemacht und verloren, aber diese Bemühungen brachten nur sehr wenig Licht in die “richtige” Herangehensweise an das Problem.
Generalisierung blieb im Großen und Ganzen ein verwirrendes Problem für den Großteil des 20. Jahrhunderts. Es war nicht einmal klar, ob es zum Bereich der Naturwissenschaften gehörte, die von Beobachtungen und Experimenten geleitet werden, oder zum Bereich der Philosophie und Mathematik, die von Logik und Selbstkonsistenz geleitet werden.
Der Raum bewegte sich weiter, bis es 1982 zu einem wegweisenden Moment kam, dem Jahr des ersten öffentlichen Prognosewettbewerbs - im Volksmund als M-Wettbewerb bekannt4. Das Prinzip war einfach: Veröffentlichen Sie einen Datensatz von 1000 abgeschnittenen Zeitreihen, lassen Sie die Teilnehmer ihre Prognosen einreichen und veröffentlichen Sie schließlich den Rest des Datensatzes (die abgeschnittenen Schwänze) zusammen mit den von den Teilnehmern erreichten Genauigkeiten. Durch diesen Wettbewerb hatte die Generalisierung, immer noch durch die Linse der Prognosegenauigkeit betrachtet, den Bereich der Naturwissenschaften betreten. In der Folge wurden Prognosewettbewerbe immer häufiger.
Einige Jahrzehnte später fügte Kaggle, gegründet im Jahr 2010, solchen Wettbewerben eine neue Dimension hinzu, indem es eine Plattform für allgemeine Vorhersageprobleme (nicht nur Zeitreihen) schuf. Stand Februar 20235 hat die Plattform 349 Wettbewerbe mit Geldpreisen organisiert. Das Prinzip bleibt dasselbe wie beim ursprünglichen M-Wettbewerb: Ein abgeschnittener Datensatz wird zur Verfügung gestellt, die Teilnehmer reichen ihre Antworten auf die gegebenen Vorhersageaufgaben ein und schließlich werden Ranglisten zusammen mit dem verborgenen Teil des Datensatzes veröffentlicht. Die Wettbewerbe gelten immer noch als der Goldstandard für die richtige Bewertung des Generalisierungsfehlers von Modellen.
Überanpassung und Unteranpassung
Überanpassung, wie sein Gegenteil Unteranpassung, ist ein Problem, das häufig bei der Erstellung eines Modells auf der Grundlage eines gegebenen Datensatzes auftritt und die Generalisierungskraft des Modells untergräbt. Historisch gesehen6 war Überanpassung das erste gut verstandene Hindernis für die Generalisierung.
Die Visualisierung von Überanpassung kann anhand eines einfachen Zeitreihenmodellierungsproblems erfolgen. Für dieses Beispiel soll angenommen werden, dass das Ziel darin besteht, ein Modell zu erstellen, das eine Reihe historischer Beobachtungen widerspiegelt. Eine der einfachsten Möglichkeiten, diese Beobachtungen zu modellieren, ist ein lineares Modell, wie unten dargestellt (siehe Abbildung 1).
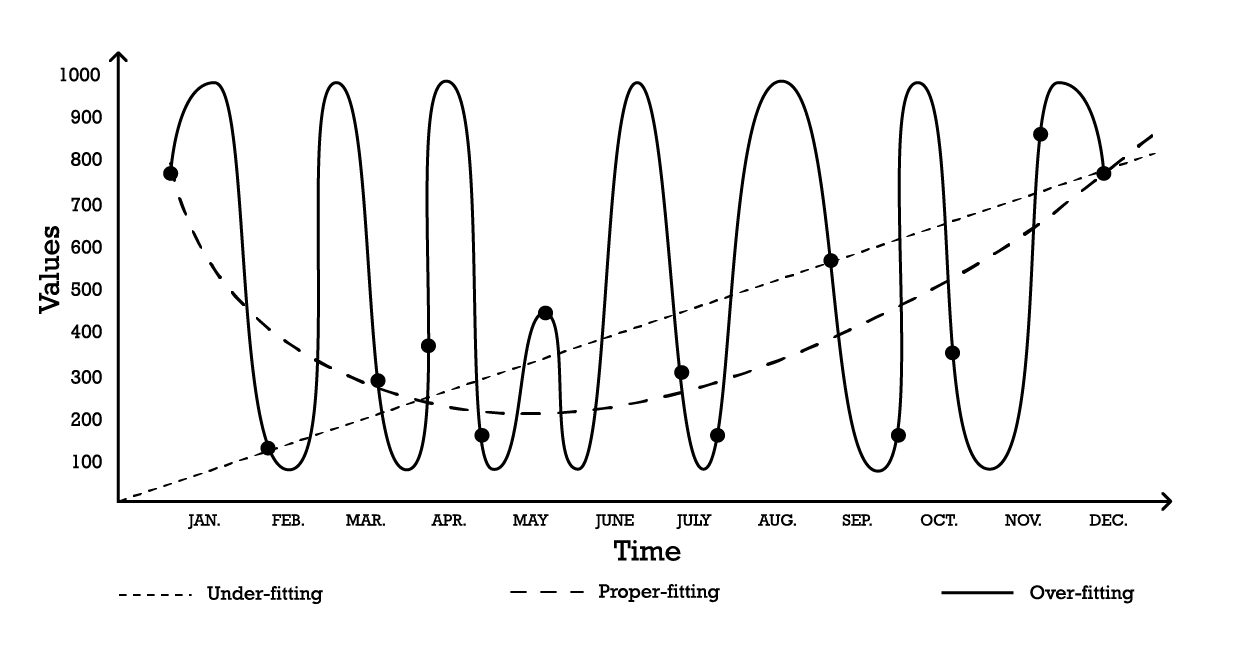
Abbildung 1: Ein zusammengesetztes Diagramm, das drei verschiedene Versuche zeigt, eine Reihe von Beobachtungen 'anzupassen'.
Das “Unteranpassungs”-Modell ist mit zwei Parametern robust, aber es passt die Daten nicht gut an, da es offensichtlich nicht die Gesamtform der Verteilung der Beobachtungen erfasst. Dieser lineare Ansatz hat eine hohe Verzerrung, aber eine geringe Varianz. In diesem Zusammenhang sollte Verzerrung als die inhärente Begrenzung der Modellierungsstrategie verstanden werden, um die Feinheiten der Beobachtungen zu erfassen, während Variance als die Empfindlichkeit gegenüber kleinen Schwankungen - möglicherweise Rauschen - der Beobachtungen verstanden werden sollte.
Ein recht komplexes Modell könnte wie die “Überanpassungs”-Kurve (Abbildung 1) angenommen werden. Dieses Modell enthält viele Parameter und passt genau zu den Beobachtungen. Dieser Ansatz hat eine geringe Verzerrung, aber eine nachweislich hohe Varianz. Alternativ könnte ein Modell mittlerer Komplexität angenommen werden, wie in der “angemessenen Anpassung”-Kurve (Abbildung 1) zu sehen ist. Dieses Modell enthält drei Parameter, hat eine mittlere Verzerrung und eine mittlere Varianz. Von diesen drei Optionen ist das angemessen angepasste Modell in Bezug auf die Generalisierung immer das beste.
Diese Modellierungsoptionen repräsentieren das Wesen des Verzerrungs-Varianz-Dilemmas.7 8 Das Verzerrungs-Varianz-Dilemma ist ein allgemeines Prinzip, das besagt, dass die Verzerrung durch Erhöhung der Varianz reduziert werden kann. Der Generalisierungsfehler wird minimiert, indem das richtige Gleichgewicht zwischen der Menge an Verzerrung und Varianz gefunden wird.
Historisch gesehen, vom frühen 20. Jahrhundert bis Anfang der 2010er Jahre, wurde ein überangepasstes Modell9 als eines definiert, das mehr Parameter enthält, als durch die Daten gerechtfertigt werden können. Tatsächlich scheint es auf den ersten Blick die perfekte Lösung für Überanpassungsprobleme zu sein, zu einem Modell zu viele Freiheitsgrade hinzuzufügen. Doch das Aufkommen des Deep Learning hat diese Intuition und die Definition von Überanpassung als irreführend erwiesen. Dieser Punkt wird im Abschnitt über Deep Double-Descent erneut aufgegriffen.
Kreuzvalidierung und Backtesting
Die Kreuzvalidierung ist eine Modellvalidierungstechnik, die verwendet wird, um zu beurteilen, wie gut ein Modell über seine unterstützenden Daten hinaus generalisieren wird. Es handelt sich um eine Unterstichprobenmethode, bei der verschiedene Teile der Daten verwendet werden, um das Modell in verschiedenen Iterationen zu testen und zu trainieren. Die Kreuzvalidierung ist das A und O moderner Vorhersagepraktiken, und nahezu alle Gewinner von Vorhersagewettbewerben machen umfangreichen Gebrauch von Kreuzvalidierung.
Es gibt zahlreiche Varianten der Kreuzvalidierung. Die beliebteste Variante ist die k-fache Validierung, bei der die ursprüngliche Stichprobe zufällig in k Unterstichproben aufgeteilt wird. Jede Unterstichprobe wird einmal als Validierungsdaten verwendet, während der Rest - alle anderen Unterstichproben - als Trainingsdaten verwendet werden.
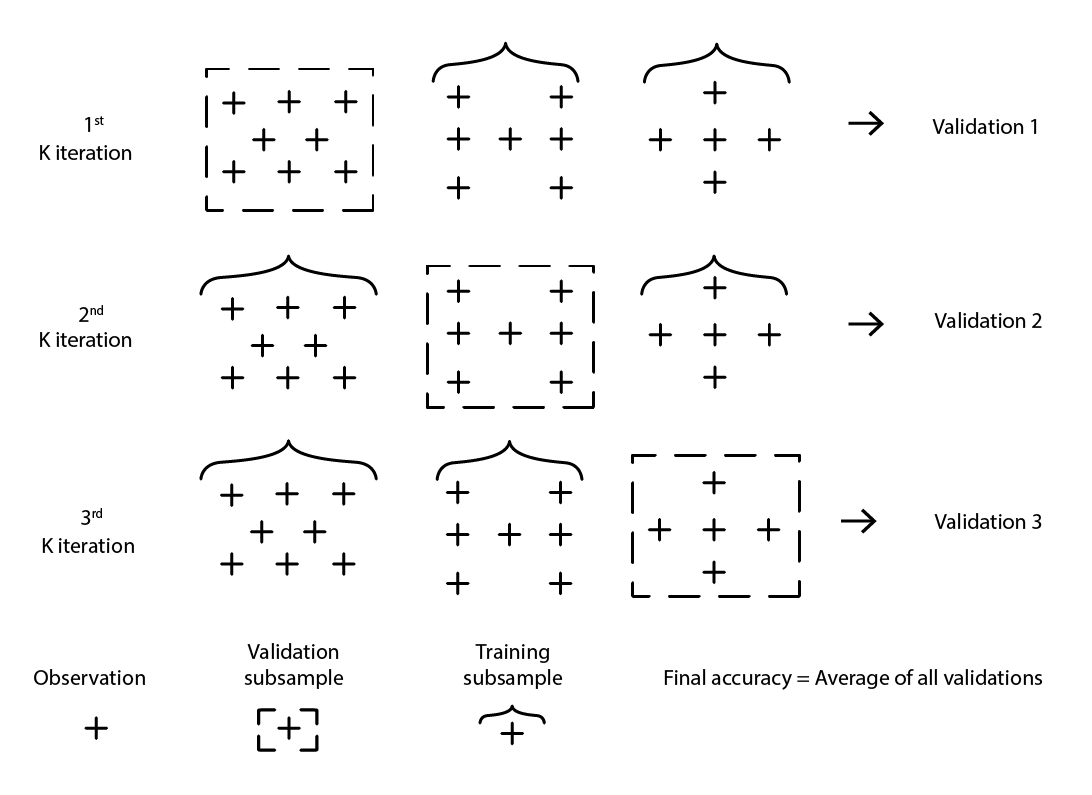
Abbildung 2: Eine Beispiel-K-Fach-Validierung. Die oben gezeigten Beobachtungen stammen alle aus demselben Datensatz. Die Technik erstellt also Datenunterstichproben für Validierungs- und Trainingszwecke.
Die Wahl des Werts k, der Anzahl der Unterstichproben, ist ein Kompromiss zwischen marginalen statistischen Gewinnen und den Anforderungen in Bezug auf Rechenressourcen. Tatsächlich wachsen die Rechenressourcen mit k-facher Validierung linear mit dem Wert k, während die Vorteile in Bezug auf Fehlerreduktion extrem abnehmende Erträge aufweisen10. In der Praxis ist die Auswahl eines Werts von 10 oder 20 für k in der Regel “gut genug”, da die statistischen Gewinne, die mit höheren Werten verbunden sind, den zusätzlichen Aufwand in Bezug auf den höheren Verbrauch von Rechenressourcen nicht wert sind.
Die Kreuzvalidierung geht davon aus, dass der Datensatz in eine Reihe unabhängiger Beobachtungen zerlegt werden kann. In der Supply Chain ist dies jedoch häufig nicht der Fall, da der Datensatz in der Regel eine Art historisierter Daten widerspiegelt, bei denen eine zeitliche Abhängigkeit vorliegt. In Anwesenheit von Zeit muss die Trainingsunterstichprobe strikt als “vorhergehend” der Validierungsunterstichprobe durchgesetzt werden. Mit anderen Worten, die “Zukunft” im Verhältnis zum Resampling-Cutoff darf nicht in die Validierungsunterstichprobe durchsickern.
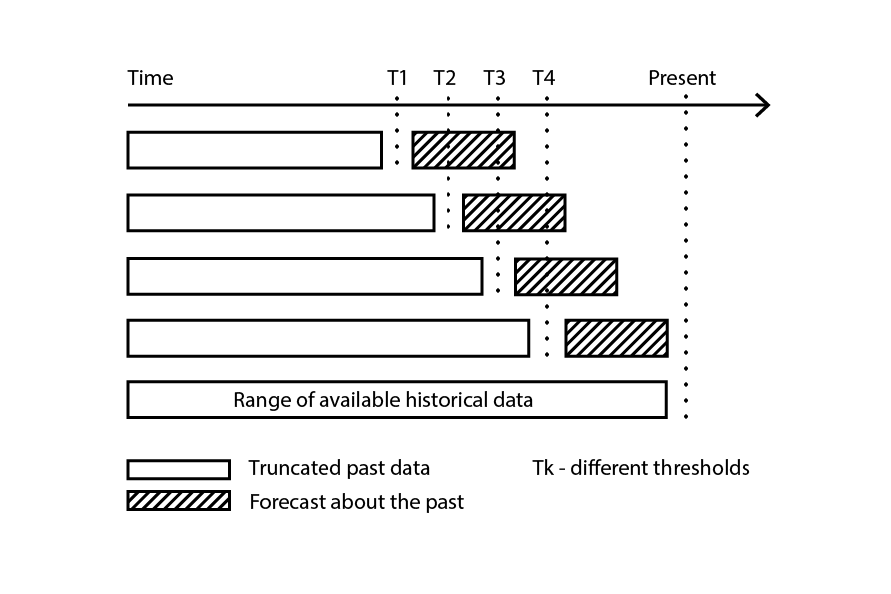
Abbildung 3: Ein Beispiel für einen Backtesting-Prozess, der Datenunterstichproben für Validierungs- und Trainingszwecke erstellt.
Backtesting stellt die Variante der Kreuzvalidierung dar, die sich direkt mit der zeitlichen Abhängigkeit befasst. Anstatt zufällige Unterstichproben zu betrachten, werden Trainings- und Validierungsdaten durch einen Cutoff erhalten: Beobachtungen vor dem Cutoff gehören zu den Trainingsdaten, während Beobachtungen nach dem Cutoff zu den Validierungsdaten gehören. Der Prozess wird durch Auswahl einer Reihe von unterschiedlichen Cutoff-Werten wiederholt.
Die Resampling-Methode, die sowohl der Kreuzvalidierung als auch dem Backtesting zugrunde liegt, ist ein leistungsstarker Mechanismus, um die Modellierungsbemühungen in Richtung einer größeren Verallgemeinerung zu lenken. Tatsächlich ist sie so effizient, dass es eine ganze Klasse von (Maschinen-)Lernalgorithmen gibt, die diesen Mechanismus in ihrem Kern nutzen. Die bekanntesten sind Random Forests und Gradient Boosted Trees.
Überwindung der dimensional Barrier
Ganz natürlich führt mehr Daten zu mehr Informationen, aus denen gelernt werden kann. Daher sollten bei ansonsten gleichen Bedingungen mehr Daten zu besseren Modellen führen oder zumindest zu Modellen, die nicht schlechter sind als ihre Vorgänger. Schließlich kann man im Notfall immer die Daten ignorieren, wenn mehr Daten das Modell schlechter machen. Aufgrund von Überanpassungsproblemen blieb das Verwerfen von Daten jedoch bis Ende der 1990er Jahre die “kleinere Übel”-Lösung. Dies war das Kernproblem der “dimensionalen Barrieren”. Diese Situation war sowohl verwirrend als auch zutiefst unbefriedigend. Durchbrüche in den 1990er Jahren haben die dimensionalen Barrieren mit beeindruckenden Erkenntnissen, sowohl theoretisch als auch praktisch, durchbrochen. Dabei gelang es diesen Durchbrüchen, - durch reine Ablenkungskraft - das gesamte Forschungsfeld für ein Jahrzehnt zu entgleisen und die Einführung ihrer Nachfolger, insbesondere der Deep-Learning-Methoden, zu verzögern, die im nächsten Abschnitt diskutiert werden.
Um besser zu verstehen, was früher mit mehr Daten haben falsch war, betrachten wir das folgende Szenario: Ein fiktiver Hersteller möchte die Anzahl der ungeplanten Reparaturen pro Jahr an großen Industrieanlagen vorhersagen. Nach sorgfältiger Überlegung des Problems hat das Engineering-Team drei unabhängige Faktoren identifiziert, die zu den Ausfallraten beitragen zu scheinen. Die jeweiligen Beiträge jedes Faktors zur Gesamtausfallrate sind jedoch unklar.
Daher wird ein einfaches lineares Regressionsmodell mit 3 Eingangsvariablen eingeführt. Das Modell kann wie folgt geschrieben werden: Y = a1 * X1 + a2 * X2 + a3 * X3, wobei
- Y die Ausgabe des linearen Modells ist (die Ausfallrate, die die Ingenieure vorhersagen möchten)
- X1, X2 und X3 die drei Faktoren sind (spezifische Arten von Arbeitsbelastungen, ausgedrückt in Betriebsstunden), die zu den Ausfällen beitragen können
- a1, a2 und a3 die drei Modellparameter sind, die identifiziert werden sollen.
Die Anzahl der Beobachtungen, die erforderlich sind, um “gut genug” Schätzungen für die drei Parameter zu erhalten, hängt weitgehend vom Rauschpegel in der Beobachtung ab und davon, was als “gut genug” gilt. Intuitiv wären jedoch mindestens zwei Dutzend Beobachtungen erforderlich, um drei Parameter anzupassen, selbst in den günstigsten Situationen. Da die Ingenieure in der Lage sind, 100 Beobachtungen zu sammeln, regeln sie erfolgreich 3 Parameter, und das resultierende Modell scheint “gut genug” zu sein, um praktisches Interesse zu wecken. Das Modell erfasst viele Aspekte der 100 Beobachtungen nicht und ist daher nur eine grobe Annäherung, aber wenn dieses Modell durch Gedankenexperimente gegen andere Situationen herausgefordert wird, sagen Intuition und Erfahrung den Ingenieuren, dass das Modell vernünftig zu funktionieren scheint.
Basierend auf ihrem ersten Erfolg beschließen die Ingenieure, tiefer zu untersuchen. Dieses Mal nutzen sie die volle Palette elektronischer Sensoren, die in den Maschinen eingebettet sind, und durch die von diesen Sensoren erzeugten elektronischen Aufzeichnungen erweitern sie den Satz der Eingangsfaktoren auf 10.000. Ursprünglich bestand der Datensatz aus 100 Beobachtungen, wobei jede Beobachtung durch 3 Zahlen charakterisiert wurde. Jetzt wurde der Datensatz erweitert; es sind immer noch die gleichen 100 Beobachtungen, aber es gibt 10.000 Zahlen pro Beobachtung.
Wenn die Ingenieure jedoch versuchen, denselben Ansatz auf ihren stark erweiterten Datensatz anzuwenden, funktioniert das lineare Modell nicht mehr. Da es 10.000 Dimensionen gibt, hat das lineare Modell 10.000 Parameter; und die 100 Beobachtungen reichen bei weitem nicht aus, um so viele Parameter zu regeln. Das Problem besteht nicht darin, dass es unmöglich ist, Parameterwerte zu finden, die passen, sondern genau das Gegenteil: Es ist trivial geworden, endlose Parametermengen zu finden, die die Beobachtungen perfekt passen. Keines dieser “passenden” Modelle ist jedoch von praktischem Nutzen. Diese “großen” Modelle passen perfekt zu den 100 Beobachtungen, aber außerhalb dieser Beobachtungen werden die Modelle unsinnig.
Die Ingenieure stehen vor der dimensionalen Barriere: Offensichtlich müssen die Anzahl der Parameter im Vergleich zu den Beobachtungen klein bleiben, sonst bricht der Modellierungsversuch zusammen. Dieses Problem ist ärgerlich, da der “größere” Datensatz mit 10.000 Dimensionen anstelle von 3 offensichtlich informativer ist als der kleinere. Ein geeignetes statistisches Modell sollte daher in der Lage sein, diese zusätzlichen Informationen zu erfassen, anstatt dysfunktional zu werden, wenn es damit konfrontiert wird.
Mitte der 1990er Jahre sorgte ein zweifacher Durchbruch11, sowohl theoretisch als auch experimentell, für Aufsehen in der Gemeinschaft. Der theoretische Durchbruch war die Vapnik-Chervonenkis (VC)-Theorie12. Die VC-Theorie zeigte, dass unter Berücksichtigung bestimmter Arten von Modellen der reale Fehler durch die Summe des empirischen Fehlers plus des strukturellen Risikos, einer intrinsischen Eigenschaft des Modells selbst, nach oben begrenzt werden konnte. In diesem Zusammenhang ist der “reale Fehler” der Fehler, der bei den Daten auftritt, die man nicht hat, während der “empirische Fehler” der Fehler ist, der bei den Daten auftritt, die man hat. Durch Minimierung der Summe des empirischen Fehlers und des strukturellen Risikos konnte der reale Fehler minimiert werden, da er “eingesperrt” war. Dies stellte sowohl ein beeindruckendes Ergebnis als auch den wohl größten Schritt in Richtung Verallgemeinerung seit der Identifizierung des Überanpassungsproblems selbst dar.
Auf experimenteller Ebene wurden Modelle eingeführt, die später als Support Vector Machines (SVMs) bekannt wurden und fast wie eine Lehrbuchableitung dessen waren, was die VC-Theorie über das Lernen identifiziert hatte. Diese SVMs wurden die ersten weit verbreiteten Modelle, die zufriedenstellend mit Datensätzen umgehen konnten, bei denen die Anzahl der Dimensionen die Anzahl der Beobachtungen überstieg.
Durch das “Einsperren” des realen Fehlers, ein wirklich überraschendes theoretisches Ergebnis, hatte die VC-Theorie die dimensionale Barriere durchbrochen - etwas, das fast ein Jahrhundert lang quälend geblieben war. Sie ebnete auch den Weg für Modelle, die hochdimensionale Daten nutzen konnten. Doch schon bald wurden SVMs selbst durch alternative Modelle verdrängt, hauptsächlich Ensemble-Methoden (Random Forests13 und Gradient Boosting), die sich in den frühen 2000er Jahren als überlegene Alternativen14 sowohl in Bezug auf Verallgemeinerung als auch auf Rechenanforderungen erwiesen. Wie die von ihnen ersetzten SVMs profitieren auch Ensemble-Methoden von theoretischen Garantien in Bezug auf ihre Fähigkeit, Überanpassung zu vermeiden. All diese Methoden haben gemeinsam, dass sie nichtparametrische Methoden sind. Die dimensionale Barriere wurde durch die Einführung von Modellen durchbrochen, die nicht für jede Dimension einen oder mehrere Parameter einführen mussten und somit einen bekannten Weg zu Überanpassungsproblemen umgingen.
Wenn wir zum zuvor erwähnten Problem der ungeplanten Reparaturen zurückkehren, im Gegensatz zu den klassischen statistischen Modellen - wie der linearen Regression, die an der dimensionalen Barriere scheitert - würden Ensemble-Methoden trotz der Tatsache, dass es nur 100 Beobachtungen gibt, von dem großen Datensatz mit seinen 10.000 Dimensionen profitieren. Darüber hinaus würden Ensemble-Methoden mehr oder weniger “out of the box” hervorragende Ergebnisse erzielen. Operativ gesehen war dies eine bemerkenswerte Entwicklung, da es nicht mehr erforderlich war, Modelle akribisch zu gestalten, indem man die genau richtige Menge an Eingabedimensionen auswählte.
Der Einfluss auf die breitere Gemeinschaft, sowohl innerhalb als auch außerhalb der akademischen Welt, war enorm. Die meisten Forschungsanstrengungen in den frühen 2000er Jahren konzentrierten sich darauf, diese nichtparametrischen “theoriegestützten” Ansätze zu erkunden. Doch die Erfolge verpufften recht schnell im Laufe der Jahre. Tatsächlich sind die besten Modelle aus der sogenannten statistischen Lernperspektive auch zwanzig Jahre später immer noch dieselben - sie profitieren lediglich von leistungsfähigeren Implementierungen15.
Der tiefe Doppelabfall
Bis 2010 galt die herkömmliche Weisheit, dass die Anzahl der Parameter viel kleiner sein musste als die Anzahl der Beobachtungen, um Überanpassungsprobleme zu vermeiden. Tatsächlich war es aufgrund der Tatsache, dass jeder Parameter implizit einen Freiheitsgrad repräsentierte, ein Rezept für Überanpassung, genauso viele Parameter wie Beobachtungen zu haben16. Ensemble-Methoden umgingen das Problem, indem sie von Anfang an nichtparametrisch waren. Doch diese entscheidende Erkenntnis stellte sich als falsch heraus, und zwar spektakulär.
Was später als der Deep Learning-Ansatz bekannt wurde, überraschte die gesamte Gemeinschaft durch hyperparametrische Modelle. Das sind Modelle, die nicht überanpassen, aber viele Male mehr Parameter als Beobachtungen enthalten.
Die Entstehung des Deep Learning ist komplex und lässt sich auf die frühesten Versuche zurückführen, die Prozesse des Gehirns, nämlich neuronale Netzwerke, zu modellieren. Die Entschlüsselung dieser Entstehung ist jedoch nicht Gegenstand der vorliegenden Diskussion. Es ist jedoch erwähnenswert, dass die Deep Learning-Revolution der frühen 2010er Jahre gerade dann begann, als das Feld das neuronale Netzwerk-Metapher zugunsten von mechanischem Verständnis aufgab. Die Deep Learning-Implementierungen ersetzten die vorherigen Modelle durch viel einfachere Varianten. Diese neueren Modelle nutzten alternative Computing-Hardware, insbesondere GPUs (Graphics Processing Units), die sich zufälligerweise als gut geeignet für die linearen Algebra-Operationen erwiesen, die Deep Learning-Modelle charakterisieren17.
Es dauerte fast weitere fünf Jahre, bis Deep Learning als Durchbruch anerkannt wurde. Ein beträchtlicher Teil der Zurückhaltung kam aus dem Lager des statistischen Lernens - zufälligerweise der Teil der Gemeinschaft, der bereits zwei Jahrzehnte zuvor die dimensionale Barriere erfolgreich durchbrochen hatte. Während die Erklärungen für diese Zurückhaltung variieren, trug der offensichtliche Widerspruch zwischen der konventionellen Überanpassungsweisheit und den Behauptungen des Deep Learning sicherlich zu einem spürbaren Maß an anfänglicher Skepsis gegenüber dieser neueren Klasse von Modellen bei.
Der Widerspruch blieb weitgehend ungelöst, bis 2019 das Deep Double Descent identifiziert wurde18, ein Phänomen, das das Verhalten bestimmter Klassen von Modellen charakterisiert. Bei solchen Modellen führt eine Erhöhung der Anzahl der Parameter zunächst zu einer Verschlechterung des Testfehlers (durch Überanpassung), bis die Anzahl der Parameter groß genug wird, um den Trend umzukehren und den Testfehler wieder zu verbessern. Der “zweite Abstieg” (des Testfehlers) war kein Verhalten, das von der Bias-Tradeoff-Perspektive vorhergesagt wurde.
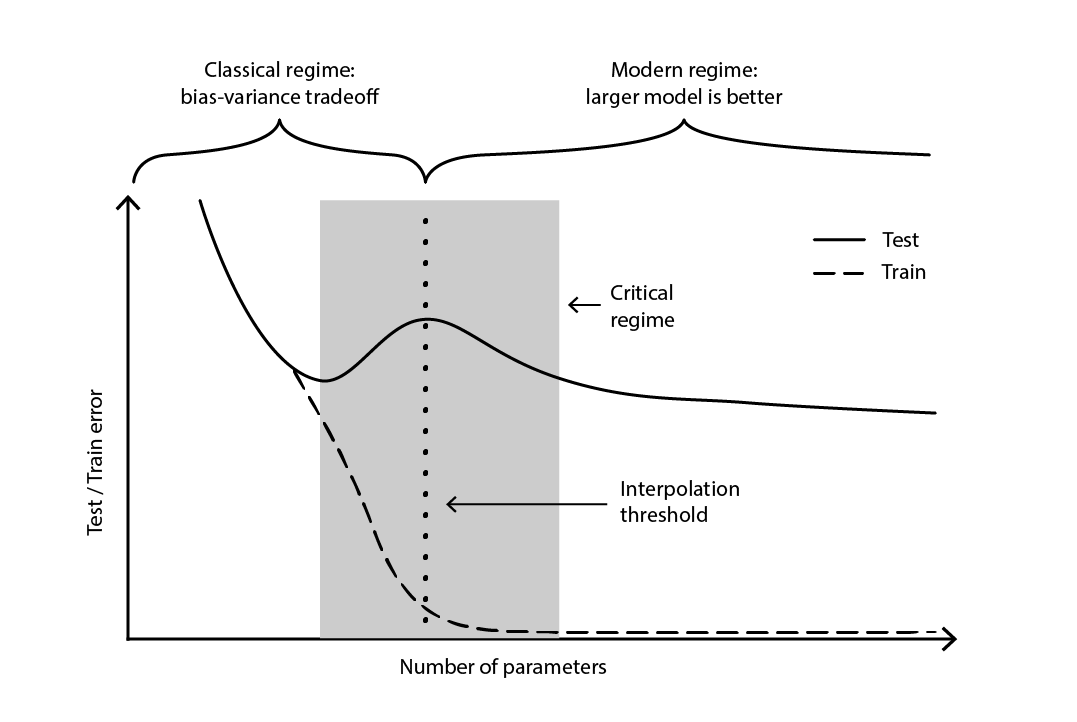
Abbildung 4. Ein tiefes Doppelabstieg.
Abbildung 4 veranschaulicht die beiden oben beschriebenen aufeinanderfolgenden Regime. Das erste Regime ist der klassische Bias-Varianz-Tradeoff, der scheinbar mit einer “optimalen” Anzahl von Parametern einhergeht. Doch dieses Minimum erweist sich als lokales Minimum. Es gibt ein zweites Regime, das beobachtbar ist, wenn man die Anzahl der Parameter weiter erhöht und das eine asymptotische Konvergenz zu einem tatsächlich optimalen Testfehler für das Modell aufweist.
Das Deep Double Descent hat nicht nur die statistische und die Deep Learning-Perspektive versöhnt, sondern auch gezeigt, dass die Generalisierung relativ wenig verstanden wird. Es hat bewiesen, dass die weit verbreiteten Theorien - bis in die späten 2010er Jahre allgemein üblich - eine verzerrte Perspektive auf die Generalisierung darstellen. Das Deep Double Descent bietet jedoch noch keinen Rahmen - oder etwas Ähnliches -, das die Generalisierungsfähigkeiten (oder das Fehlen davon) von Modellen aufgrund ihrer Struktur vorhersagen würde. Bis heute bleibt der Ansatz entschieden empirisch.
Die Dornen der Supply Chain
Wie ausführlich behandelt, ist die Generalisierung äußerst herausfordernd, und Supply Chains werfen ihre eigenen Eigenheiten ein, die die Situation weiter verschärfen. Erstens kann die von den Praktikern der Datenversorgungskette gesuchte Datenversorgungskette für immer unzugänglich bleiben; nicht nur teilweise unsichtbar, sondern vollständig unbeobachtbar. Zweitens kann allein der Akt der Vorhersage die Zukunft verändern und die Gültigkeit der Vorhersage beeinflussen, da Entscheidungen auf diesen Vorhersagen aufbauen. Daher sollte bei der Herangehensweise an die Generalisierung im Kontext einer Supply Chain ein zweigleisiger Ansatz verwendet werden: Ein Bein ist die statistische Stichhaltigkeit des Modells, das andere ist das hochrangige Denken, das das Modell unterstützt.
Darüber hinaus ist die verfügbare Datenmenge nicht immer die gewünschte Datenmenge. Betrachten Sie einen Hersteller, der die Nachfrage prognostizieren möchte, um die zu produzierenden Mengen zu entscheiden. Es gibt keine solche Sache wie historische “Nachfrage” Daten. Stattdessen stellt die historische Verkaufsdaten die beste verfügbare Näherung dar, um die historische Nachfrage widerzuspiegeln. Die historischen Verkäufe werden jedoch durch vergangene Fehlbestände verzerrt. Nullverkäufe, verursacht durch Fehlbestände, sollten nicht mit Nullnachfrage verwechselt werden. Während ein Modell entwickelt werden kann, um diese Verkaufshistorie in eine Art Nachfragehistorie zu korrigieren, ist der Generalisierungsfehler dieses Modells von vornherein schwer fassbar, da weder die Vergangenheit noch die Zukunft diese Daten enthalten. Kurz gesagt, “Nachfrage” ist ein notwendiger, aber immaterieller Begriff.
In der Sprache des maschinellen Lernens ist die Modellierung der Nachfrage ein unüberwachtes Lernproblem, bei dem die Ausgabe des Modells niemals direkt beobachtet wird. Dieser unüberwachte Aspekt macht die meisten Lernalgorithmen und die meisten Modellvalidierungstechniken zunichte - zumindest in ihrer “naiven” Form. Darüber hinaus widerspricht es auch der Idee eines Vorhersagewettbewerbs, bei dem ein ursprünglicher Datensatz in einen öffentlichen (Trainings-) Teil und einen privaten (Validierungs-) Teil aufgeteilt wird. Die Validierung selbst wird zu einer Modellierungsaufgabe, aus Notwendigkeit.
Einfach ausgedrückt, die Prognose, die vom Hersteller erstellt wird, wird die Zukunft, die der Hersteller erlebt, auf die eine oder andere Weise prägen. Eine hohe prognostizierte Nachfrage bedeutet, dass der Hersteller die Produktion hochfahren wird. Wenn das Geschäft gut geführt wird, werden wahrscheinlich Skaleneffekte im Produktionsprozess erreicht, was die Produktionskosten senkt. Der Hersteller wird voraussichtlich von diesen neuen wirtschaftlichen Vorteilen profitieren, um die Preise zu senken und so einen Wettbewerbsvorteil gegenüber Konkurrenten zu erlangen. Der Markt, der nach der günstigsten Option sucht, kann diesen Hersteller schnell als die wettbewerbsfähigste Option annehmen und so eine Nachfragesteigerung auslösen, die weit über die ursprüngliche Prognose hinausgeht.
Dieses Phänomen wird als selbsterfüllende Prophezeiung bezeichnet, eine Vorhersage, die aufgrund des Einflusses des Glaubens der Teilnehmer an die Vorhersage selbst tendenziell wahr wird. Eine unkonventionelle, aber nicht völlig unvernünftige Perspektive würde Lieferketten als riesige, selbsterfüllende Rube Goldberg-Maschinen charakterisieren. Auf methodologischer Ebene kompliziert diese Verflechtung von Beobachter und Beobachtung die Situation weiter, da die Generalisierung mit der Erfassung der strategischen Absicht verbunden wird, die den Entwicklungen in der Lieferkette zugrunde liegt.
An diesem Punkt mag die Herausforderung der Generalisierung in der Lieferkette unüberwindbar erscheinen. Tabellenkalkulationen, die in Lieferketten allgegenwärtig sind, deuten sicherlich darauf hin, dass dies die Standardposition der meisten Unternehmen ist, wenn auch implizit. Eine Tabelle ist jedoch in erster Linie ein Werkzeug, um die Lösung des Problems auf ein ad-hoc menschliches Urteil zu verschieben, anstatt die Anwendung einer systematischen Methode.
Obwohl die Verlagerung auf menschliches Urteil in sich selbst immer die falsche Antwort ist, ist sie auch keine zufriedenstellende Antwort auf das Problem. Das Vorhandensein von Fehlbeständen bedeutet nicht, dass alles erlaubt ist, was die Nachfrage betrifft. Sicherlich wäre es höchst unwahrscheinlich, dass (beobachtete) Nachfrage während der letzten drei Jahre 10-mal höher als die Verkäufe gewesen sein könnte, wenn der Hersteller durchschnittliche Servicelevel von über 90% aufrechterhalten hat. Daher ist es vernünftig zu erwarten, dass eine systematische Methode entwickelt werden kann, um solche Verzerrungen zu bewältigen. Auch die selbsterfüllende Prophezeiung kann modelliert werden, insbesondere durch den Begriff der Politik, wie er von der Regelungstechnik verstanden wird.
Bei der Betrachtung einer realen Lieferkette erfordert die Generalisierung einen zweigleisigen Ansatz. Erstens muss das Modell statistisch fundiert sein, soweit es die breiten “Lern"wissenschaften zulassen. Dies umfasst nicht nur theoretische Perspektiven wie klassische Statistik und statistisches Lernen, sondern auch empirische Bestrebungen wie maschinelles Lernen und Vorhersagewettbewerbe. Die Rückkehr zur Statistik des 19. Jahrhunderts ist kein vernünftiger Vorschlag für eine Lieferkettenpraxis im 21. Jahrhundert.
Zweitens muss das Modell durch hochrangiges Denken unterstützt werden. Mit anderen Worten, für jede Komponente des Modells und jeden Schritt des Modellierungsprozesses sollte es eine Begründung geben, die aus Sicht der Lieferkette Sinn ergibt. Ohne diese Zutat ist operatives Chaos19 fast garantiert, normalerweise ausgelöst durch eine Entwicklung der Lieferkette selbst, ihres Betriebsumfelds oder ihrer zugrunde liegenden Anwendungslandschaft. Tatsächlich besteht der ganze Sinn des hochrangigen Denkens nicht darin, ein Modell einmalig zum Funktionieren zu bringen, sondern es nachhaltig über mehrere Jahre in einer sich ständig verändernden Umgebung zum Funktionieren zu bringen. Dieses Denken ist die nicht so geheime Zutat, die dabei hilft zu entscheiden, wann es an der Zeit ist, das Modell zu überarbeiten, wenn sein Design, was auch immer es ist, nicht mehr mit der Realität und/oder den Geschäftszielen übereinstimmt.
Aus der Ferne betrachtet scheint dieser Vorschlag anfällig für die frühere Kritik zu sein, die gegenüber Tabellenkalkulationen geäußert wurde - die Kritik, harte Arbeit einem schwer fassbaren “menschlichen Urteil” zu überlassen. Obwohl dieser Vorschlag immer noch die Bewertung des Modells dem menschlichen Urteil überlässt, ist die Ausführung des Modells als vollständig automatisiert gedacht. Daher sollen die täglichen Operationen vollständig automatisiert sein, auch wenn die laufenden Engineering-Bemühungen zur weiteren Verbesserung der numerischen Rezepte dies nicht sind.
Anmerkungen
-
Es gibt eine wichtige algorithmische Technik namens “Memoisierung”, die genau ein Ergebnis durch sein vorberechnetes Ergebnis ersetzt, das also mehr Speicher gegen weniger Berechnung tauscht. Diese Technik ist jedoch für die vorliegende Diskussion nicht relevant. ↩︎
-
Warum die meisten veröffentlichten Forschungsergebnisse falsch sind, John P. A. Ioannidis, August 2005 ↩︎
-
Aus der Perspektive der Zeitreihenprognose wird der Begriff der Generalisierung über das Konzept der “Genauigkeit” angegangen. Genauigkeit kann als ein Spezialfall der “Generalisierung” betrachtet werden, wenn man Zeitreihen in Betracht zieht. ↩︎
-
Makridakis, S.; Andersen, A.; Carbone, R.; Fildes, R.; Hibon, M.; Lewandowski, R.; Newton, J.; Parzen, E.; Winkler, R. (April 1982). “The accuracy of extrapolation (time series) methods: Results of a forecasting competition”. Journal of Forecasting. 1 (2): 111–153. doi:10.1002/for.3980010202. ↩︎
-
Kaggle in Zahlen, Carl McBride Ellis, abgerufen am 8. Februar 2023, ↩︎
-
Der 1935er Auszug “Vielleicht sind wir altmodisch, aber für uns scheint eine sechsfache Analyse basierend auf dreizehn Beobachtungen eher wie Überanpassung”, aus “The Quarterly Review of Biology” (Sep, 1935 Volume 10, Number 3pp. 341 - 377), scheint darauf hinzuweisen, dass das statistische Konzept der Überanpassung zu dieser Zeit bereits etabliert war. ↩︎
-
Grenander, Ulf. Über die empirische spektrale Analyse stochastischer Prozesse. Ark. Mat., 1(6):503– 531, 08 1952. ↩︎
-
Whittle, P. Tests of Fit in Time Series, Vol. 39, No. 3/4 (Dec., 1952), pp. 309-318] (10 Seiten), Oxford University Press ↩︎
-
Everitt B.S., Skrondal A. (2010), Cambridge Dictionary of Statistics, Cambridge University Press. ↩︎
-
Die asymptotischen Vorteile der Verwendung größerer k-Werte für das k-Fold-Verfahren lassen sich aus dem zentralen Grenzwertsatz ableiten. Diese Erkenntnis legt nahe, dass wir durch Erhöhung von k etwa 1 / sqrt(k) nahe daran kommen, das gesamte Verbesserungspotenzial des k-Fold-Verfahrens auszuschöpfen. ↩︎
-
Support-Vektor-Netzwerke, Corinna Cortes, Vladimir Vapnik, Machine Learning Band 20, Seiten 273–297 (1995) ↩︎
-
Die Vapnik-Chernovenkis (VC)-Theorie war nicht der einzige Ansatz, um zu formalisieren, was “Lernen” bedeutet. Valiants PAC (probably approximately correct)-Framework von 1984 ebnete den Weg für formale Lernansätze. Das PAC-Framework hatte jedoch nicht die immense Traktion und die operativen Erfolge, die die VC-Theorie um die Jahrtausendwende genoss. ↩︎
-
Random Forests, Leo Breiman, Machine Learning Band 45, Seiten 5–32 (2001) ↩︎
-
Eine der unglücklichen Folgen davon, dass Support Vector Machines (SVMs) stark von einer mathematischen Theorie inspiriert sind, besteht darin, dass diese Modelle wenig “mechanisches Verständnis” für moderne Computerhardware haben. Die relative Unzulänglichkeit von SVMs bei der Verarbeitung großer Datensätze - einschließlich Millionen von Beobachtungen oder mehr - im Vergleich zu Alternativen führte zum Niedergang dieser Methoden. ↩︎
-
XGBoost und LightGBM sind zwei Open-Source-Implementierungen der Ensemble-Methoden, die in der Machine-Learning-Gemeinschaft weiterhin weit verbreitet sind. ↩︎
-
Um der Kürze willen wird hier etwas vereinfacht. Es gibt ein ganzes Forschungsfeld, das sich mit der “Regularisierung” statistischer Modelle befasst. In Anwesenheit von Regularisierungseinschränkungen kann die Anzahl der Parameter, selbst bei einem klassischen Modell wie einer linearen Regression, sicher die Anzahl der Beobachtungen überschreiten. In Anwesenheit von Regularisierung repräsentiert kein Parameterwert mehr einen vollen Freiheitsgrad, sondern nur noch einen Bruchteil davon. Daher wäre es angemessener, von der Anzahl der Freiheitsgrade zu sprechen, anstatt von der Anzahl der Parameter. Da diese tangentialen Überlegungen die hier dargelegten Ansichten nicht grundlegend verändern, genügt die vereinfachte Version. ↩︎
-
Tatsächlich ist die Kausalität umgekehrt. Die Pioniere des Deep Learnings schafften es, ihre ursprünglichen Modelle - neuronale Netzwerke - in einfachere Modelle umzubauen, die fast ausschließlich auf linearer Algebra beruhten. Der Zweck dieser Umgestaltung bestand genau darin, es möglich zu machen, diese neueren Modelle auf Computerhardware auszuführen, die Vielseitigkeit gegen rohe Leistung, nämlich GPUs, eintauschte. ↩︎
-
Deep Double Descent: Wo größere Modelle und mehr Daten schaden, Preetum Nakkiran, Gal Kaplun, Yamini Bansal, Tristan Yang, Boaz Barak, Ilya Sutskever, Dezember 2019 ↩︎
-
Die überwiegende Mehrheit der datenwissenschaftlichen Initiativen in der Supply Chain scheitert. Meine oberflächlichen Beobachtungen deuten darauf hin, dass die Unkenntnis der Datenwissenschaftler darüber, was die Supply Chain antreibt, die Hauptursache für die meisten dieser Misserfolge ist. Obwohl es für einen neu ausgebildeten Datenwissenschaftler unglaublich verlockend ist, das neueste und glänzendste Open-Source-Machine-Learning-Paket zu nutzen, sind nicht alle Modellierungstechniken gleichermaßen geeignet, um das hochrangige Denken zu unterstützen. Tatsächlich sind die meisten “mainstream” Techniken geradezu schlecht, wenn es um den Whiteboxing-Prozess geht. ↩︎