Sicherheitsbestand
Der Sicherheitsbestand ist eine Methode zur Optimierung des Lagerbestands, die angibt, wie viel Bestand über die erwartete Nachfrage hinaus aufbewahrt werden muss, um ein bestimmtes Service-Level-Ziel zu erreichen. Der zusätzliche Bestand dient als “Sicherheitspuffer” - daher der Name - um das Unternehmen vor erwarteten zukünftigen Schwankungen zu schützen. Die Sicherheitsbestandsformel hängt sowohl von der erwarteten zukünftigen Nachfrage als auch von der erwarteten zukünftigen Lieferzeit ab. Die Unsicherheit wird für beide Faktoren als normalverteilt angenommen. Die Sicherheitsbestandsformel ist in den meisten Bestandsmanagement-Systemen weit verbreitet, einschließlich der bekanntesten ERPs und MRPs.
Update Juli 2020: Der unten beschriebene Ansatz ist eine “klassische” Supply Chain, leider erweist er sich auch als äußerst dysfunktional. Insbesondere sind weder die zukünftige Nachfrage noch die zukünftige Lieferzeit normalverteilt (d.h. keine Gaußsche Verteilung). Darüber hinaus verfehlt die gesamte Perspektive völlig den Punkt, dass alle vom Unternehmen bestellbaren oder produzierbaren Artikel um die gleichen Ressourcen konkurrieren. Wir raten dringend davon ab, ein Sicherheitsbestandsmodell in realen Lieferketten zu verwenden.
Zielgruppe: Dieses Dokument richtet sich in erster Linie an Supply Chain-Experten im Einzelhandel oder in der Fertigung. Dennoch ist dieses Dokument auch nützlich für Buchhaltungs-/ERP-/eCommerce-Softwarehersteller, die ihre Anwendungen um Lagerverwaltungsfunktionen erweitern möchten.
Wir haben versucht, die mathematischen Anforderungen so gering wie möglich zu halten, aber wir können nicht ganz auf Formeln verzichten, da der genaue Zweck dieses Dokuments darin besteht, ein praktischer Leitfaden zu sein, der erklärt, wie der Sicherheitsbestand berechnet wird.
Download: calculate-safety-stocks.xls (Microsoft Excel-Tabelle)
Einführung
Das Bestandsmanagement ist ein finanzieller Kompromiss zwischen Lagerhaltungskosten und Fehlbestandskosten. Je mehr Bestand vorhanden ist, desto mehr Betriebskapital wird benötigt und desto höher ist die Wertminderung des Bestands. Andererseits führt ein zu geringer Bestand zu Lagerbeständen, die zu fehlenden potenziellen Verkäufen führen und möglicherweise den gesamten Produktionsprozess unterbrechen.
Der Lagerbestand hängt im Wesentlichen von zwei Faktoren ab:
- Leitnachfrage: die Menge an Artikeln, die verbraucht oder gekauft werden.
- Durchlaufzeit: die Verzögerung zwischen der Entscheidung zur Nachbestellung und der erneuten Verfügbarkeit.
Doch diese beiden Faktoren unterliegen Unsicherheiten:
- Nachfrageschwankungen: Das Kundenverhalten kann sich auf eher unvorhersehbare Weise entwickeln.
- Durchlaufzeitschwankungen: Lieferanten oder Transportunternehmen können mit ungeplanten Schwierigkeiten konfrontiert sein.
Die Entscheidung über den Sicherheitsbestand entspricht implizit einem Kompromiss zwischen diesen Kosten unter Berücksichtigung der Unsicherheiten.
Das Gleichgewicht zwischen Lagerhaltungskosten und Fehlbestandskosten hängt sehr stark vom Geschäft ab. Anstatt diese Kosten direkt zu berücksichtigen, werden wir nun den klassischen Begriff des Service-Levels einführen.
Der Service-Level drückt die Wahrscheinlichkeit aus, dass ein bestimmter Sicherheitsbestand nicht zu einem Fehlbestand führt. Natürlich steigt der Service-Level, wenn die Sicherheitsbestände erhöht werden. Wenn die Sicherheitsbestände sehr groß werden, tendiert der Service-Level gegen 100% (d.h. eine Wahrscheinlichkeit von null, auf einen Fehlbestand zu stoßen).
Die Wahl des Service-Levels, d.h. der akzeptablen Wahrscheinlichkeit eines Fehlbestands, fällt nicht in den Rahmen dieses Leitfadens, aber wir haben einen separaten Leitfaden zur Berechnung optimaler Service-Levels.
Bestandsauffüllungsmodell
Der Nachbestellpunkt ist die Menge an Bestand, die eine Bestellung auslösen sollte. Wenn es keine Unsicherheit gäbe (d.h. die zukünftige Nachfrage wäre perfekt bekannt und die Lieferung wäre absolut zuverlässig), wäre der Nachbestellpunkt einfach gleich der gesamten prognostizierten Nachfrage während der Durchlaufzeit, auch als Durchlaufzeitnachfrage bezeichnet.
In der Praxis haben wir jedoch aufgrund der Unsicherheiten:
Nachbestellpunkt = Durchlaufzeitnachfrage + Sicherheitsbestand
Wenn wir davon ausgehen, dass die Prognosen nicht voreingenommen sind (statistisch gesehen), würde ein Sicherheitsbestand von null zu einem Service-Level von 50% führen. Tatsächlich bedeuten unvoreingenommene Prognosen, dass die zukünftige Nachfrage genauso wahrscheinlich größer oder kleiner ist als die Durchlaufzeitnachfrage (denken Sie daran, dass die Durchlaufzeitnachfrage nur ein prognostizierter Wert ist).
Vorsicht: Prognosen können unvoreingenommen sein, ohne genau zu sein. Die Voreingenommenheit deutet auf einen systematischen Fehler des Prognosemodells hin (z.B. immer eine Nachfrageüberschätzung um 20%).
Normalverteilung des Fehlers
An diesem Punkt benötigen wir eine Möglichkeit, die Unsicherheit in der Durchlaufzeitnachfrage darzustellen. Im Folgenden nehmen wir an, dass der Fehler normalverteilt ist, siehe das Bild unten.
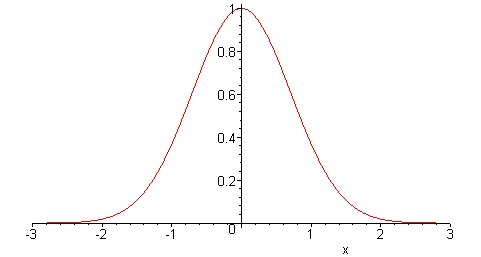
Statistische Anmerkungen: Diese Annahme einer Normalverteilung ist nicht völlig willkürlich. Unter bestimmten Bedingungen konvergieren statistische Schätzer gemäß dem Zentralen Grenzwertsatz gegen eine Normalverteilung. Aber diese Überlegungen liegen außerhalb des Rahmens dieses Leitfadens.
Eine Normalverteilung wird nur durch zwei Parameter definiert: ihren Mittelwert und ihre Varianz. Da wir davon ausgehen, dass die Prognosen unvoreingenommen sind, nehmen wir an, dass der Mittelwert der Fehlerverteilung null ist, was nicht bedeutet, dass wir von einem Fehler von null ausgehen.
Die Bestimmung der Varianz des Prognosefehlers ist eine heiklere Aufgabe. Lokad und die meisten Prognose-Toolkits bieten MAPE-Schätzungen (Mean Absolute Percentage Error) in Verbindung mit ihren Prognosen an. Um die Vollständigkeit zu wahren, werden wir erklären, wie einfache Heuristiken verwendet werden können, um dieses Problem zu lösen.
Insbesondere kann die Varianz innerhalb der historischen Daten als gute Heuristik verwendet werden, um die Varianz des Prognosefehlers abzuschätzen. David Piasecki schlägt auch vor, die prognostizierte Nachfrage anstelle der Durchschnittsnachfrage im Varianzausdruck zu verwenden, das heißt
wobei $$E$$ der Mittelwert-Operator ist, $$y_t$$ die historische Nachfrage für den Zeitraum $$t$$ (typischerweise die Verkaufsmenge) und $$y’$$ die prognostizierte Nachfrage.
Die grundlegende Idee hinter dieser Annahme ist, dass der Prognosefehler oft mit der erwarteten Variation korreliert ist: Je größer die bevorstehenden Variationen sind, desto größer ist der Fehler in den Prognosen.
Tatsächlich beinhaltet die Berechnung dieser Fehlervarianz einige Feinheiten, die im Folgenden genauer behandelt werden.
Sicherheitsbestandsausdruck
Zu diesem Zeitpunkt haben wir sowohl den Mittelwert als auch die Varianz bestimmt, daher ist die Fehlerverteilung bekannt. Wir müssen nun das akzeptable Fehlerniveau innerhalb dieser Verteilung berechnen. Hier oben haben wir die Begriffe Service-Level (eine Prozentsatz) eingeführt, um dies zu tun.
Anmerkungen: Wir nehmen eine statische Lieferzeit an. Dennoch kann ein sehr ähnlicher Ansatz für eine variable Lieferzeit verwendet werden. Siehe
Um das Service-Level in ein Fehlerlevel, auch Service-Faktor genannt, umzuwandeln, müssen wir die inverse kumulative Normalverteilung verwenden (manchmal auch inverse Normalverteilung genannt) (siehe NORMSINV für die entsprechende Excel-Funktion). Obwohl es kompliziert klingen mag, ist es das nicht, wir empfehlen, sich das Normalverteilungs-Applet anzusehen, um einen visuelleren Einblick zu erhalten. Wie Sie sehen können, wandelt die kumulative Funktion den Prozentsatz in eine Fläche unter der Kurve um, wobei der Schwellenwert auf der X-Achse dem Wert des Service-Faktors entspricht.
Intuitiv berechnen wir
Sicherheitsbestand = Standardabweichung des Fehlers * Service-Faktor
Formell sei $$S$$ der Sicherheitsbestand, dann haben wir
wobei $$\sigma$$ die Standardabweichung (d.h. die Quadratwurzel von $$\sigma^2$$, der oben definierten Varianz), $$cdf$$ die normalisierte kumulative Normalverteilung (mit Nullmittelwert und Varianz gleich eins) und $$P$$ das Service-Level ist.
Unter Berücksichtigung dessen, dass
Bestellpunkt = Lieferzeitnachfrage + Sicherheitsbestand
Sei $$R$$ der Bestellpunkt, dann haben wir
Abgleich von Lieferzeit und Prognosezeitraum
Bisher haben wir einfach angenommen, dass wir für eine gegebene Lieferzeit die entsprechende zukünftige Nachfrageprognose direkt erstellen können. In der Praxis funktioniert es jedoch nicht genau so. Die Analyse der historischen Daten beginnt normalerweise mit der Aggregation der Daten in Zeitperioden (in der Regel Wochen oder Monate).
Die gewählte Periode stimmt jedoch möglicherweise nicht genau mit der Lieferzeit überein. Daher sind weitere Berechnungen erforderlich, um die Lieferzeitnachfrage und ihre zugehörige Varianz auszudrücken (unter der Annahme, dass wir immer noch eine Normalverteilung für den Prognosefehler annehmen, wie im vorherigen Abschnitt erläutert).
Intuitiv kann die Lieferzeitnachfrage als Summe der prognostizierten Werte für die zukünftigen Perioden berechnet werden, die den Lieferzeitabschnitt schneiden. Es muss darauf geachtet werden, den letzten prognostizierten Zeitraum richtig anzupassen.
Formal sei $$T$$ die Periode und $$L$$ die Lieferzeit. Wir schreiben
wobei $$k$$ eine ganze Zahl und $$0 ≤ α < 1$$ ist. Sei $$D$$ die Lieferzeitnachfrage. Dann haben wir den endgültigen Ausdruck für die Lieferzeitnachfrage
wobei $$y’_n$$ die prognostizierte Nachfrage für die $$n$$-te Periode in der Zukunft ist.
Unter Berücksichtigung der gleichen Annahmen über die Normalverteilung können wir die Varianz des Prognosefehlers wie folgt berechnen:
wobei $$y’$$ der durchschnittliche Prognosewert pro Periode ist
Dennoch wird $$\sigma^2$$ hier als pro Periode berechnete Varianz berechnet, während wir eine Varianz benötigen, die zur Lieferzeit passt. Sei $$\sigma_{L}^2$$ die angepasste pro Lieferzeit Varianz, dann haben wir
Schließlich können wir den Bestellpunkt wie folgt neu ausdrücken
Verwendung von Excel zur Berechnung des Bestellpunkts
In diesem Abschnitt wird erläutert, wie der Bestellpunkt mit Microsoft Excel berechnet wird. Wir empfehlen, einen Blick auf die Beispiel-Excel-Tabelle zu werfen, die bereitgestellt wird.
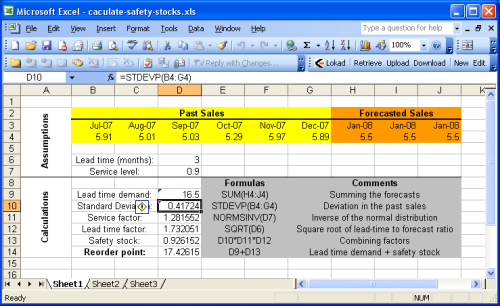
Die Beispieltabelle ist im Wesentlichen in zwei Abschnitte unterteilt: die Annahmen oben und die Berechnungen unten. Die Prognosen werden als Teil der Annahmen betrachtet, da die Umsatz- (oder Nachfrage-) Prognose über den Rahmen dieses Leitfadens hinausgeht. Weitere Informationen finden Sie in unserem Tutorial zur Umsatzprognose mit Microsoft Excel.
Die meisten in dem vorherigen Abschnitt eingeführten Formeln sind sehr einfache Operationen (Additionen, Multiplikationen), die mit Microsoft Excel sehr einfach durchzuführen sind. Es gibt jedoch zwei bemerkenswerte Funktionen:
- NORMSINV (Microsoft KB): schätzt die kumulative Normalverteilung, hier als cdf bezeichnet.
- STDEV (Microsoft KB): schätzt die Standardabweichung, hier als $$σ$$ bezeichnet. Wir erinnern daran, dass die Standardabweichung $$σ$$ die Quadratwurzel der Varianz $${σ^2}$$ ist.
Aus Gründen der Einfachheit implementiert das erste Blatt nicht die Heuristik $${σ^2 = E[ (y_t - y’)^2 ]}$$ bei der Berechnung des Servicefaktors. Dieser Ansatz wird in Sheet2 (2. Arbeitsblatt des Excel-Dokuments) implementiert. Da wir in diesem Beispiel stationäre Prognosen angenommen haben, bleibt der Bestellpunkt unabhängig von dieser Heuristik identisch.
Ressourcen
Inventory Management and Production Planning and Scheduling, Edward A. Silver, David F. Pyke, Rein Peterson, Wiley; 3. Auflage, 1998